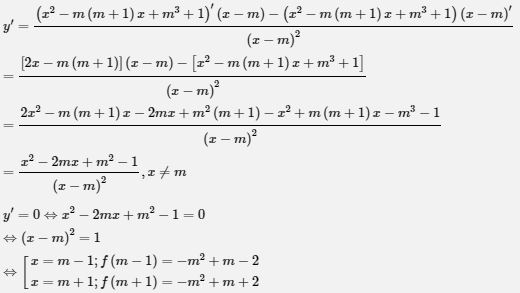Bài 15 trang 17 SGK Đại số và Giải tích 12 Nâng caoChứng minh rằng với mọi giá trị của m, hàm số luôn có cực đại và cực tiểu GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn Quảng cáo
Đề bài Chứng minh rằng với mọi giá trị của \(m\), hàm số: \(y = {{{x^2} - m\left( {m + 1} \right)x + {m^3} + 1} \over {x - m}}\) luôn có cực đại và cực tiểu. Lời giải chi tiết TXĐ: \(D = {\mathbb{R}}\backslash \left\{ m \right\}\)
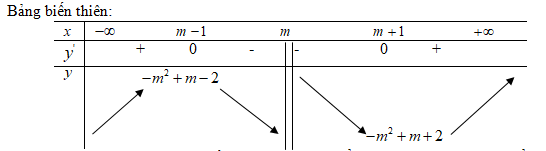
Với mọi giá trị của \(m\), hàm số đạt cực đại tại điểm \(x=m-1\) và đạt cực tiểu tại điểm \(x=m+1\) Chú ý: Ta có thể viết lại hàm số f(x) để tính đạo hàm cho đơn giản như sau: \(\begin{array}{l} Loigiaihay.com
|