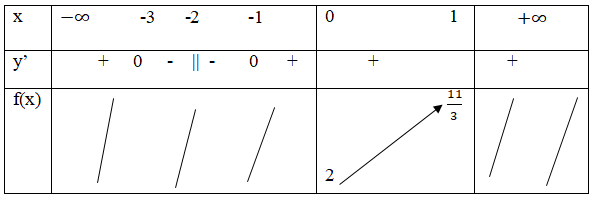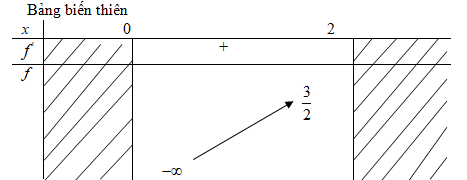Bài 17 trang 22 SGK Đại số và Giải tích 12 Nâng cao

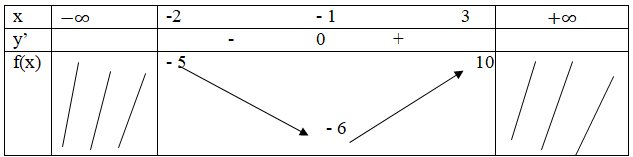
LG a

\(f\left( x \right) = {x^2} + 2x - 5\) trên đoạn \(\left[ { - 2;3} \right]\);

Lời giải chi tiết:

\(D = \left[ { - 2;3} \right]\)

\(f'\left( x \right) = 2x + 2\)

\(f'\left( x \right) = 0 \Leftrightarrow  x=- 1 \in \left[ { - 2;3} \right]\)

Ta có: \(f\left( { - 2} \right) =  - 5;f\left( { - 1} \right) =  - 6;\) \(f\left( 3 \right) = 10\).

Vậy: \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ { - 2;3} \right]}  =  - 6;\mathop {\max \,f\left( x \right) = 10}\limits_{x \in \left[ { - 2;3} \right]} \).

Cách khác:

Hàm số f(x)= x² + 2x – 5

Tập xác định D = R.

Đạo hàm y’= 2x +2 = 0 ⇔ x = - 1

Bảng biến thiên:

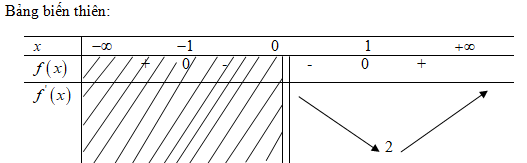
Vậy: \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ { - 2;3} \right]}  =  - 6;\mathop {\max \,f\left( x \right) = 10}\limits_{x \in \left[ { - 2;3} \right]} \).

LG b

\(f\left( x \right) = {{{x^3}} \over 3} + 2{x^2} + 3x - 4\) trên đoạn \(\left[ { - 4;0} \right]\);

Lời giải chi tiết:

\(D = \left[ { - 4;0} \right]\)

\(f'\left( x \right) = {x^2} + 4x + 3\)

\(f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{
x = - 1 \in \left[ { - 4;0} \right] \hfill \cr 
x = - 3 \in \left[ { - 4;0} \right] \hfill \cr} \right.\)

Ta có: \(f\left( { - 4} \right) =  - {{16} \over 3};f\left( { - 1} \right) =  - {{16} \over 3};\) \(f\left( { - 3} \right) =  - 4;f\left( 0 \right) =  - 4\)

Vậy \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ { - 4;0} \right]}  =  - {{16} \over 3};\) \(\mathop {\max \,f\left( x \right)}\limits_{x \in \left[ { - 4;0} \right]}  =  - 4\).

LG c

\(f\left( x \right) = x + {1 \over x}\) trên đoạn \(\left( {0; + \infty } \right)\);

Lời giải chi tiết:

\(D = \left( {0; + \infty } \right)\)

\(f'\left( x \right) = 1 - {1 \over {{x^2}}} = {{{x^2} - 1} \over {{x^2}}}\) với mọi \(x \ne 0\)

\(f'\left( x \right) = 0 \Leftrightarrow x =  \pm 1\)

\(x=1\in \left( {0; + \infty } \right.)\)

\(x=-1\not\in \left( {0; + \infty } \right.)\)

Vậy \(\mathop {\min \,\,f\left( x \right) = f\left( 1 \right)}\limits_{x \in \left( {0; + \infty } \right)}  = 2\).

Hàm số không đạt giá trị lớn nhất trên khoảng \(\left( {0; + \infty } \right)\).

LG d

\(f\left( x \right) =  - {x^2} + 2x + 4\) trên đoạn \(\left[ {2;4} \right]\);

Lời giải chi tiết:

\(D = \left[ {2;4} \right]\)

\(f'\left( x \right) =  - 2x + 2\)

\(f'\left( x \right) = 0 \Leftrightarrow x = 1 \notin \left[ {2;4} \right]\)

Ta có: \(f\left( 2 \right) = 4;f\left( 4 \right) =  - 4\)

Vậy \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ {2;4} \right]}  =  - 4;\) \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ {2;4} \right]}  = 4\).

LG e

\(f\left( x \right) = {{2{x^2} + 5x + 4} \over {x + 2}}\) trên đoạn \(\left[ {0;1} \right]\);

Lời giải chi tiết:

\(D = \left[ {0;1} \right]\)

\(f'\left( x \right) = {{2{x^2} + 8x + 6} \over {{{\left( {x + 2} \right)}^2}}}\)

\(f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{
x = - 1 \notin \left[ {0;1} \right] \hfill \cr 
x = - 3 \notin \left[ {0;1} \right] \hfill \cr} \right.\)

Ta có: \(f\left( 0 \right) = 2;f\left( 1 \right) = {{11} \over 3}\)

Vậy \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ {0;1} \right]}  = 2;\) \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ {0;1} \right]}  = {{11} \over 3}\)

Cách khác:

Bảng biến thiên:

Vậy \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ {0;1} \right]}  = 2;\) \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ {0;1} \right]}  = {{11} \over 3}\)

LG f

\(f\left( x \right) = x - {1 \over x}\) trên đoạn \(\left( {0;2} \right]\);

Lời giải chi tiết:

\(D = \left( {0;2} \right]\)

\(f'\left( x \right) = 1 + {1 \over {{x^2}}} > 0\) với mọi \(x \in \left( {0;2} \right]\)

\(f\left( 2 \right) = {3 \over 2}\)

Vậy \(\mathop {\,\max f\left( x \right)}\limits_{x \in \left[ {0;2} \right]}  = {3 \over 2}\) .

Hàm số không đạt giá trị nhỏ nhất trên \(\left( {0;2} \right]\).

Loigiaihay.com