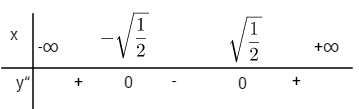Bài 47 trang 45 SGK giải tích 12 nâng caoCho hàm số: a) Khảo sát sự biến thiên và vẽ đồ thị hàm số với m = 2. b) Chứng minh rằng đồ thị hàm số đã cho luôn đi qua hai điểm cố định với mọi giá trị của m. GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
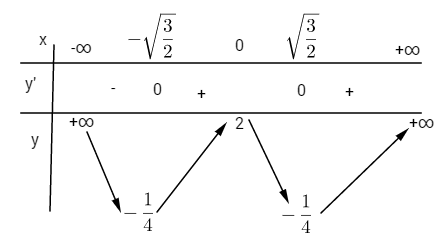
Cho hàm số: \(y = {x^4} - \left( {m + 1} \right){x^2} + m\) LG a Khảo sát sự biến thiên và vẽ đồ thị hàm số với \(m = 2\). Lời giải chi tiết: Với \(m = 2\) ta có: \(y = {x^4} - 3{x^2} + 2\) \(\eqalign{ Bảng biến thiên:
Hàm số đồng biến trên các khoảng \(\left( { - \sqrt {\frac{3}{2}} ;0} \right)\) và \(\left( {\sqrt {\frac{3}{2}} ; + \infty } \right)\) Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - \sqrt {\frac{3}{2}} } \right)\) và \(\left( {0;\sqrt {\frac{3}{2}} } \right)\) Hàm số đạt cực đại tại \(x = 0\) và \({y_{CD}} = 2\) Hàm số đạt cực tiểu tại \(x = \pm \sqrt {\frac{3}{2}} \) và \({y_{CT}} = - \frac{1}{4}\) \(y'' = 12{x^2} - 6\) \(y'' = 0 \Leftrightarrow x = \pm \sqrt {{1 \over 2}} ;\,y\left( { \pm \sqrt {{1 \over 2}} } \right) = {3 \over 4}\)
Đồ thị có hai điểm uốn : \({I_1}\left( { - \sqrt {{1 \over 2}} ;{3 \over 4}} \right)\) và \({I_2}\left( {\sqrt {{1 \over 2}} ;{3 \over 4}} \right)\) Điểm đặc biệt \(y = 0 \Leftrightarrow \left[ \matrix{
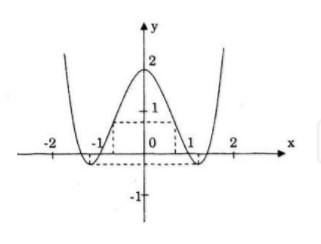
Đồ thị: Đồ thị nhận trục tung làm trục đối xứng. LG b Chứng minh rằng đồ thị hàm số đã cho luôn đi qua hai điểm cố định với mọi giá trị của \(m\). Lời giải chi tiết: Đồ thị của hàm số đã cho đi qua điểm \(\left( {{x_o};{y_o}} \right)\) khi và chỉ khi \({y_o} = x_o^4 - \left( {m + 1} \right)x_o^2 + m \) \(\begin{array}{l} \(\Leftrightarrow \left( {1 - x_o^2} \right)m + x_o^4 - x_o^2 - {y_o} = 0\,\,\left( 1 \right)\) Đồ thị đi qua điểm \(\left( {{x_o};{y_o}} \right)\) với moi giá trị của \(m\) khi và chỉ khi phương trình \((1)\) nghiệm đúng với mọi \(m\), tức là: \( \left\{ \begin{array}{l} \( \Leftrightarrow \left\{ \begin{array}{l} \( \Leftrightarrow \left\{ \matrix{ Vậy với mọi giá trị của m, đồ thị của hàm số đã cho luôn đi qua hai điểm cố định \((-1;0)\) và \((1;0)\). Loigiaihay.com
|