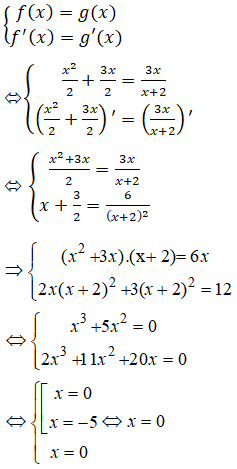Bài 60 trang 56 SGK giải tích 12 nâng caoChứng minh rằng các đồ thị của hai hàm số: tiếp xúc với nhau. Xác định tiếp điểm của hai đường cong trên và viết phương trình tiếp tuyến chung tại điểm đó. GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn Quảng cáo
Đề bài Chứng minh rằng các đồ thị của hai hàm số: \(f\left( x \right) = {{{x^2}} \over 2} + {3 \over 2}x\) và \(g\left( x \right) = {{3x} \over {x + 2}}\) tiếp xúc với nhau. Xác định tiếp điểm của hai đường cong trên và viết phương trình tiếp tuyến chung tại điểm đó. Phương pháp giải - Xem chi tiết Hai đường cong f(x) và g(x) tiếp xúc nhau nếu hệ sau có nghiệm: \(\left\{ \begin{array}{l} Nghiệm của hệ trên chính là hoành độ tiếp điểm. Lời giải chi tiết Hoành độ tiếp điểm của hai đường cong đã cho là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l} \(\eqalign{ \(\begin{array}{l} Thay x=0 và x=-5 vào (2) ta được: +) \(x=0\) thì \(VT=0 + \frac{3}{2} = \frac{3}{2} = \frac{6}{{{{\left( {0 + 2} \right)}^2}}}=VP\) nên x=0 thỏa mãn (2) Do đó x=0 là nghiệm của hệ. Vậy hệ có \(1\) nghiệm duy nhất \(x = 0\) suy ra y=0. Vậy hai đường cong tiếp xúc với nhau tại gôc tọa độ \(O\); \(y'\left( 0 \right) = {3 \over 2}\). Phương trình tiếp tuyến chung của hai đường cong tại điểm gốc là \(y = {3 \over 2}x.\) Cách khác: Các em có thể giải trực tiếp hệ trên mà không cần thay như sau:
Loigiaihay.com
|