Bài 9 trang 28 SGK Hình học 12Cho hình hộp ABCD.A'B'C'D'. Tỉ số thể tích của khối tứ diện ACB'D' và khối hộp ABCD.A'B'C'D' bằng: GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn Quảng cáo
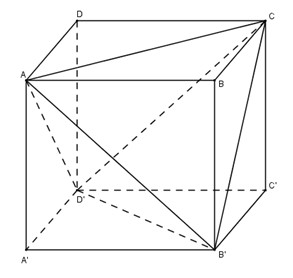
Đề bài Cho hình hộp \(ABCD.A'B'C'D'\). Tỉ số thể tích của khối tứ diện \(ACB'D'\) và khối hộp \(ABCD.A'B'C'D'\) bằng: (A) \(\displaystyle {1 \over 2}\) (B) \(\displaystyle{1 \over 3}\) (C) \(\displaystyle{1 \over 4}\) (D) \(\displaystyle{1 \over 6}\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết Phân chia và lắp ghép các khối đa diện. Hình hộp được chia thành \(5\) khối \(A’.AB'D';\, B.AB’C;\, C’.B’CD’;\, D.ACD’ \) và \(ACB’D’.\) Lời giải chi tiết
Giả sử diện tích đáy hình hộp là: \(S\) chiều cao là \(h\) Thể tích hình hộp là \(V=Sh\) Hình hộp được chia thành \(5\) khối tứ diện \(A’.AB'D';\) \( B.AB’C;;\) \( C’.B’CD’;\) \( D.ACD’\) và \(ACB’D’.\) Ta có: \({V_{A'.AB'D'}} = {V_{A.A'B'D'}}\) \( = \dfrac{1}{3}.h.{S_{A'B'D'}} = \dfrac{1}{3}h.\dfrac{1}{2}S\) \( = \dfrac{1}{6}.Sh = \dfrac{1}{6}.V\) Tương tự \({V_{B.AB'C}} = {V_{C'.B'CD'}} = {V_{D.ACD'}} = \dfrac{1}{6}V\) Do đó \({V_{ACB'D'}} = V - \;({V_{A'AB'D'}} + {V_{BAB'C}} + {V_{C'B'CD'}} + {V_{DACD'}})\) \(\begin{array}{l} = V - \left( {\dfrac{1}{6}V + \dfrac{1}{6}V + \dfrac{1}{6}V + \dfrac{1}{6}V} \right)\\ = V - \dfrac{2}{3}V\\ = \dfrac{1}{3}V\\ \Rightarrow \dfrac{{{V_{ACB'D'}}}}{V} = \dfrac{1}{3}\end{array}\) Chọn (B). loigiaihay.com
|