Đề bài
Cho tam giác \(ABC\), các đường trung tuyến \(BD\) và \(CE\). Chọn câu đúng.
-
A.
\(BD + CE < \dfrac{3}{2}BC\)
-
B.
\(BD + CE > \dfrac{3}{2}BC\)
-
C.
\(BD + CE = \dfrac{3}{2}BC\)
-
D.
\(BD + CE = BC\)
Phương pháp giải
+ Sử dụng tính chất đường trung tuyến của tam giác và quan hệ giữa các cạnh trong tam giác
Lời giải của GV Loigiaihay.com
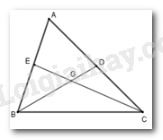
Gọi \(G\) là giao điểm của \(BD\) và \(CE\). Trong \(\Delta GBC\) ta có \(BG + CG > BC\)
Ta lại có \(BG = \dfrac{2}{3}BD;\,CG = \dfrac{2}{3}CE\) (tính chất các đường trung tuyến của tam giác \(ABC\))
Từ đó \(\dfrac{2}{3}BD + \dfrac{2}{3}CE > BG + CG\)\( \Rightarrow \dfrac{2}{3}\left( {BD + CE} \right) > BC\)\( \Rightarrow BD + CE > \dfrac{3}{2}BC.\)
Đáp án : B

Các bài tập cùng chuyên đề

















