Đề bài
Cho tam giác \(ABC\) vuông tại \(A\). Gọi \(M\), N, \(P\) lần lượt là trung điểm thuộc các cạnh \(AB\), AC, \(BC\) và \(MP = \frac{{AC}}{2}\), \(MP\;{\rm{//}}\;AN\).Tứ giác \(AMPN\) là hình gì?
-
A.
Hình thang.
-
B.
Hình thang cân.
-
C.
Hình chữ nhật.
-
D.
Hình thang vuông.
Phương pháp giải
Chứng minh tứ giác AMPN là hình bình hành có \(\widehat A = {90^o}\) nên tứ giác AMPN là hình chữ nhật.
Lời giải của GV Loigiaihay.com
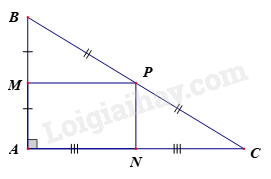
Xét tam giác ABC ta có: \(MP = \frac{{AC}}{2}\), \(MP\;{\rm{//}}\;AN\)
Mà \(AN = \frac{{AC}}{2}\) \( \Rightarrow MP\;{\rm{ = }}\;AN\)
\( \Rightarrow \) Tứ giác \(AMPN\) là hình bình hành
Mà \(\widehat A = {90^o}\)\( \Rightarrow AMPN\) là hình chữ nhật.
Đáp án : C

Các bài tập cùng chuyên đề

















