Cho hình vuông ABCD. Trên cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?

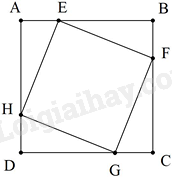
Ta có: AH = BE = CF = DG

suy ra \(\Delta AEH = \Delta BFE = \Delta CGF = \Delta DHG(c.g.c)\)

Do đó: EH = FE = GF = HG (1)

Lại có: \(\Delta AEH = \Delta BFE \) suy ra \(\widehat {{{BEF}}} = \widehat {AHE}\)

Mà \(\widehat {AEH} + \widehat {AHE} = 90^0\) (tổng hai góc nhọn của tam giác vuông)

suy ra \( \widehat {AEH} + \widehat {{{BEF}}} = {90^0}\) nên \( \widehat {FEH} = 180^0 - 90^0 = {90^0}\) (2)

Từ (1) và (2) suy ra tứ giác EFGH là hình vuông.

Hình thoi có một góc vuông là hình vuông.