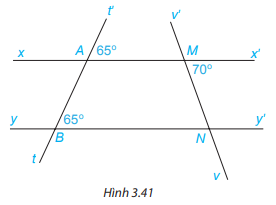
Cho Hình 3.41.
a) Giải thích tại sao xx’//yy’.
b) Tính số đo góc MNB.
a) Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.
b) Sử dụng tính chất của 2 đường thẳng song song
a) Vì \(\widehat {t'AM} = \widehat {ABN}( = 65^\circ )\), mà 2 góc này ở vị trí đồng vị nên xx’//yy’ (Dấu hiệu nhận biết 2 đường thẳng song song.)
b) Vì xx’//yy’ nên \(\widehat {x'MN} = \widehat {MNB}\) (2 góc so le trong), mà \(\widehat {x'MN} = 70^\circ \) suy ra \(\widehat {MNB} = 70^\circ \)

Các bài tập cùng chuyên đề
Bài 1 :
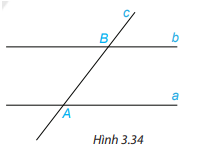
Vẽ hai đường thẳng song song a,b. Kẻ đường thẳng c cắt đường thẳng a tại A và cắt đường thẳng b tại B. Trên Hình 3.34:
a) Em hãy đo một cặp góc so le trong rồi rút ra nhận xét.
b) Em hãy đo một cặp góc đồng vị rồi rút ra nhận xét.
Bài 2 :
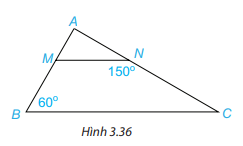
1. Cho Hình 3.36, biết MN//BC, \(\widehat {ABC} = 60^\circ ,\widehat {MNC} = 150^\circ \).
Hãy tính số đo các góc BMN và ACB.
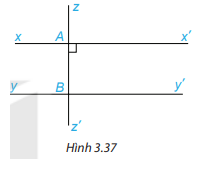
2. Cho Hình 3.37, biết rằng xx’//yy’ và zz’ \( \bot \) xx’. Tính số đo góc ABy và cho biết zz’ có vuông góc với yy’ không
Bài 3 :
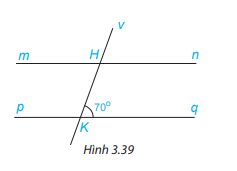
Cho Hình 3.39, biết rằng mn//pq. Tính số đo các góc Mhk, VHn.
Bài 4 :
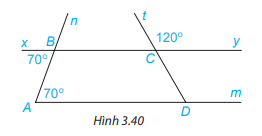
Cho Hình 3.40
a) Giải thích tại sao Am//By.
b) Tính \(\widehat {CDm}\)
Bài 5 :
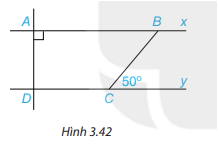
Cho Hình 3.42, biết rằng Ax//Dy, \(\widehat A = 90^\circ ,\widehat {BCy} = 50^\circ \). Tính số đo các góc ADC và ABC.
Bài 6 :
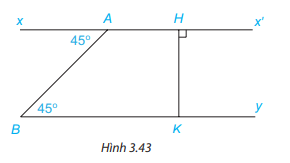
Cho Hình 3.43. Giải thích tại sao:
a) Ax’ // By
b) By \( \bot \) HK
Bài 7 :
Cho hình thang ABCD có cạnh AD vuông góc với hai đáy AB và CD. Số đo góc ở đỉnh B gấp đôi số đo góc ở đỉnh C. Tính số đo các góc của hình thang đó.
Bài 8 :
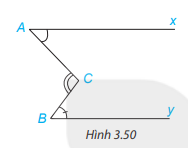
Cho Hình 3.50, trong đó hai tia Ax và By nằm trên hai đường thẳng song song. Chứng minh rằng \(\widehat C = \widehat A + \widehat B\)
Bài 9 :
Em hãy:
- Vẽ hai đường thẳng a và b song song với nhau.
- Vẽ đường thẳng c cắt đường thẳng a và b lần lượt tại A và B.
a) Chọn và đo một cặp góc so le trong, so sánh cặp góc này.
b) Chọn và đo một cặp góc đồng vị, so sánh cặp góc này.
Bài 10 :
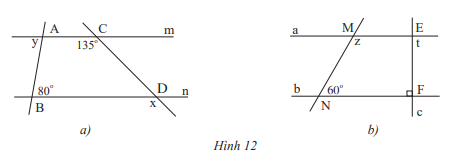
Cho biết m // n và a // b. Tính số đo x,y,z và t của các góc trong hình 12.
Bài 11 :
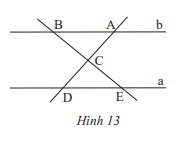
Tìm các cặp góc bằng nhau của hai tam giác ABC và DEC trong Hình 13, biết a // b.
Bài 12 :
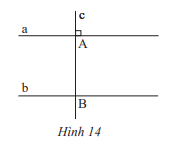
Cho hai đường thẳng a, b song song với nhau, đường thẳng c vuông góc với a tại A và cắt b tại B. Hãy giải thích tại sao đường thẳng c cũng vuông góc với b.
Bài 13 :
Trong Hình 15, cho biết a // b, Tìm số đo các góc đỉnh A và B
Bài 14 :
Vẽ một đường thẳng cắt hai đường thẳng sao cho trong các góc tạo thành có một cặp góc so le trong bằng nhau. Đặt tên cho các góc đó.
a) Vì sao cặp góc so le trong còn lại cũng bằng nhau?
b) Vì sao các cặp góc đồng vị cũng bằng nhau?
Bài 15 :
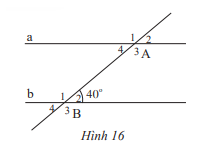
Cho Hình 16, biết a // b.
a) Chỉ ra góc ở vị trí so le trong, đồng vị với \(\widehat {{B_2}}\)
b) Tính số đo \(\widehat {{A_4}},\widehat {{A_2}},\widehat {{B_3}}\)
c) Tính số đo \(\widehat {{B_1}},\widehat {{A_1}}\).
Bài 16 :
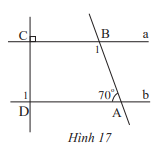
Cho Hình 17, biết a // b.
Tính số đo các góc \(\widehat {{B_1}}\) và \(\widehat {{D_1}}\)
Bài 17 :
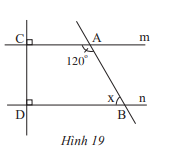
Quan sát Hình 19 và cho biết:
a) Vì sao m // n?
b) Số đo x của góc \(\widehat {ABD}\) là bao nhiêu?
Bài 18 :
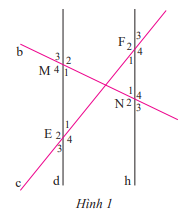
Quan sát Hình 1, biết d // h. Hãy kể tên một số cặp góc bằng nhau có trong Hình 1
Bài 19 :
Cho Hình 6, biết hai đường thẳng a và b song song với nhau và \(\widehat {{A_1}} = 50^\circ \)
a) Hãy viết tên các cặp góc so le trong và các cặp góc đồng vị.
b) Tính số đo của \(\widehat {{A_3}},\widehat {{B_3}}\)
c) Kẻ đường thẳng c vuông góc với đường thẳng a tại M. Chứng minh rằng c \( \bot \) b.
Bài 20 :
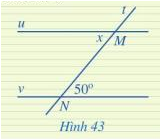
Tìm số đo x trong Hình 43, biết u // v
Bài 21 :
Quan sát hình 44, biết a // b.
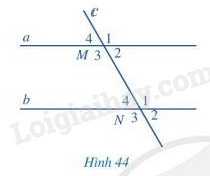
a) So sánh \(\widehat {{M_1}}\) và \(\widehat {{N_3}}\); \(\widehat {{M_4}}\) và \(\widehat {{N_2}}\) ( mỗi cặp góc M1 và N3, M4 và N2 gọi là một cặp góc so le ngoài)
b) Tính: \(\widehat {{M_2}} + \widehat {{N_1}}\) và \(\widehat {{M_3}} + \widehat {{N_4}}\) ( mỗi cặp góc M2 và N1, M3 và N4 gọi là một cặp góc trong cùng phía)
Bài 22 :
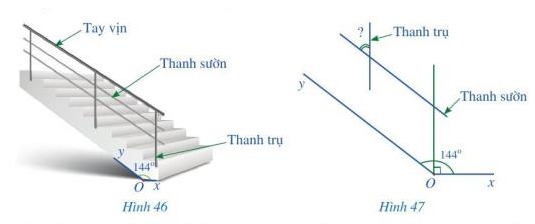
Để đảm bảo an toàn khi đi lại trên cầu thang của ngôi nhà, người ta phải làm lan can. Phía trên của lan can có tay vịn làm chỗ dựa để khi lên xuống cầu thang được thuận tiện. Phía dưới tay vịn là các thanh trụ song song với nhau và các thanh sườn song song với nhau. Để đảm bảo chắc chắn thì các thanh trụ của lan can được gắn vuông góc cố định xuống bậc cầu thang.
Trong Hình 46, góc xOy bằng 144\(^\circ \). Hỏi góc nhọn tạo bởi một thanh sườn với một thanh trụ của lan can là bao nhiêu độ?
Bài 23 :
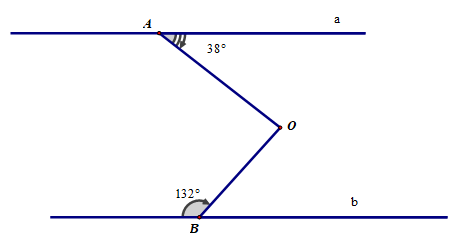
Cho hình vẽ. Biết : a//b, hãy tính số đo của góc AOB.
Bài 24 :
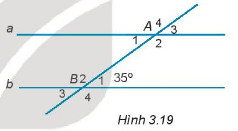
Cho hình 3.19,biết \(a// b\)
a) Tính số đo góc \({A_1}\).
b) So sánh góc \({A_4}\) và góc \({B_2}\).
c) Tính số đo góc \({A_2}\)
Bài 25 :
Vẽ lại hình 3.20 vào vở.
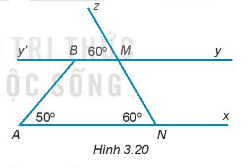
a) Giải thích tại sao \(Ax\parallel By.\)
b) Tính số đo góc \(ABy'\).
c) Tính số đo góc ABM.
Bài 26 :
Vẽ lại Hình 3.22 vào vở:
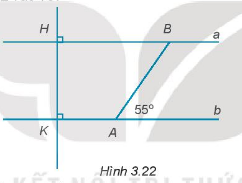
a) Giải thích tại sao \(a//b\)
b) Tính số đo góc ABH.
Bài 27 :
Cho hình 3.24.
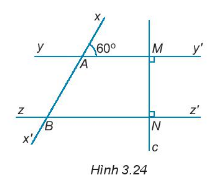
a) Giải thích tại sao \(yy'\parallel zz'\).
b) Tính số đo góc ABz.
c) Vẽ tia phân giác At của góc MAB, tia At cắt đường thẳng zz’ tại H. Tính số đo góc AHN.
Bài 28 :
Cho hình 3.25
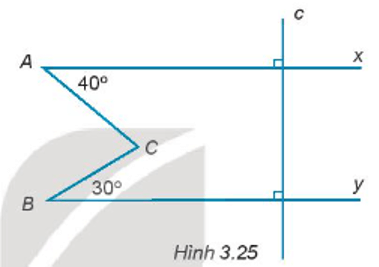
a) Giải thích tại sao \(Ax// By\).
b) Tính số đo góc ACB.
Bài 29 :
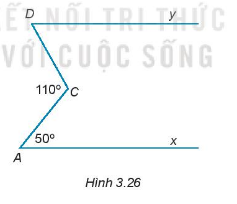
Cho hình 3.26, biết \(Ax\parallel Dy,\widehat {xAC} = {50^\circ};\widehat {ACD} = {110^\circ}\). Tính số đo góc CDy.
Bài 30 :
Cho hình 3.8.
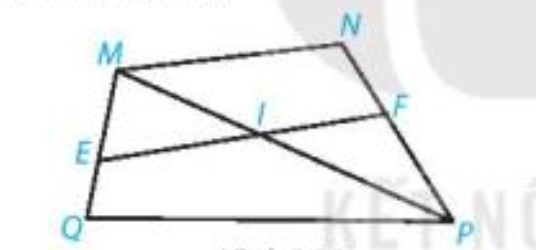
a) Tìm các góc ở vị trí so le trong với góc FIP, góc NMI.
b) Tìm các góc đồng vị với góc EQP, góc IFP.