Phương trình \(\cot x =  - 1\) có nghiệm là:

A.\( - \frac{\pi }{4} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\)

B.\(\frac{\pi }{4} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\)

C.\(\frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)

D.\( - \frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)

Bài 1 :

Tập xác định của hàm số \(y = \cot \left( {x + \frac{\pi }{6}} \right) + \sqrt {\frac{{1 + \cos x}}{{1 - \cos x}}} \) là:

Bài 2 :

Tập xác định của hàm số \(y = \tan \left( {2x - \frac{\pi }{3}} \right)\) là

Bài 3 :

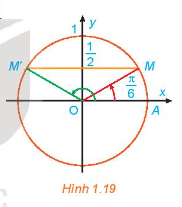
a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoảng \(\left[ {0;2\pi } \right)\)

b) Dựa vào tính tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho.

Bài 4 :

Giải các phương trình sau: a) \(\sin x = \frac{{\sqrt 2 }}{2}\);        b) \(\sin 3x =  - \sin 5x\)

Bài 5 :

Khi mặt trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được Mặt Trời chiếu sáng một phần. Các pha của Mặt Trăng mô tả mức độ phần bề mặt của nó được Mặt Trời chiếu sáng. Khi góc giữa Mặt Trời, Trái Đất và Mặt Trăng là \(\alpha \left( {{0^0} \le \;\alpha  \le {{360}^0}} \right)\)thì tỉ lệ F của phần Mặt Trăng được chiếu sáng cho bới công thức:

\(F = \frac{1}{2}\left( {1 - \cos \alpha } \right)\).

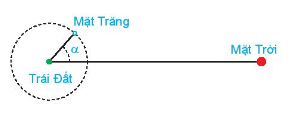
Xác định góc \(\alpha \) tương ứng với các pha sau của Mặt Trăng.

a) \(F = 0\) (trăng mới)

b) \(F = 0,25\) (trăng lưỡi liềm)

c) \(F = 0,5\) (trăng bán nguyệt đầu tháng hoặc trăng bán nguyệt cuối tháng)

d) \(F = 1\) (trăng tròn)

Bài 6 :

Giải các phương trình sau:

a) \(2\cos x =  - \sqrt 2 \);            b) \(\cos 3x - \sin 5x = 0\)

Bài 7 :

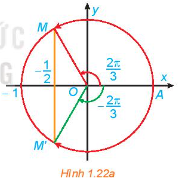
a) Quan sát Hình 1.22a, tìm các nghiệm của phương trình đã cho trong nửa khoảng \(\left[ { - \pi ;\pi } \right)\).

b) Dựa vào tính tuần hoản của hàm số cosin, hãy viết công thức nghiệm của phương trình đã cho.

Bài 8 :

Giải các phương trình sau:

a) \(\sqrt 3 \tan 2x =  - 1\);                              b) \(\tan 3x + \tan 5x = 0\)’

Bài 9 :

a) Quan sát Hình 1.24, hãy cho biết đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = \tan x\) tại mấy điểm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)?\)

b) Dựa vào tính tuần hoàn của hàm tang, hãy viết công thức nghiệm của phương trình đã cho

Bài 10 :

Giải các phương trình sau:

a) \(\cot x = 1;\)                                                           b) \(\sqrt 3 \cot x + 1 = 0\)

Bài 11 :

a) Quan sát Hình 1.25, hãy cho biết đường thẳng \(y =  - 1\) cắt đồ thị hàm số \(y = \cot x\) tại mấy điểm trên khoảng \(\left( {0;\pi } \right)?\)

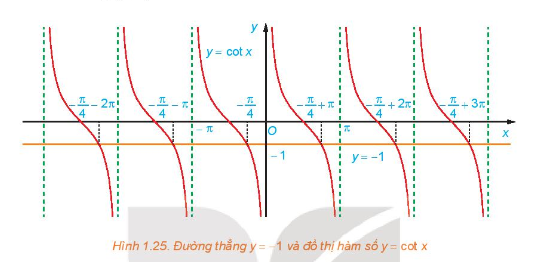
b) Dựa vào tính tuần hoàn của hàm cotang, hãy viết công thức nghiệm của phương trình đã cho.

Bài 12 :

Giải các phương trình sau:

a) \(\sin x = \frac{{\sqrt 3 }}{2}\);               

b) \(2\cos x =  - \sqrt 2 \);                  

c) \(\sqrt 3 \tan \left( {\frac{x}{2} + {{15}^0}} \right) = 1\);          

d) \(\cot \left( {2x - 1} \right) = \cot \frac{\pi }{5}\)

Bài 13 :

Giải các phương trình sau:

a) \(\sin 2x + \cos 4x = 0\);                 b) \(\cos 3x =  - \cos 7x\)

Bài 14 :

Giải phương trình \(\sin 2x = \sin \left( {x + \frac{\pi }{4}} \right)\)

Bài 15 :

a) Giải phương trình: \(\sin x = \frac{{\sqrt 3 }}{2}\)

b) Tìm góc lượng giác x sao cho \(\sin x = \sin {55^ \circ }\)

Bài 16 :

a)     Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \sin x,x \in \left[ { - \pi ;\pi } \right]\) tại hai giao điểm \({A_0},{B_0}\) (Hình 34). Tìm hoành độ của hai giao điểm \({A_0},{B_0}\).

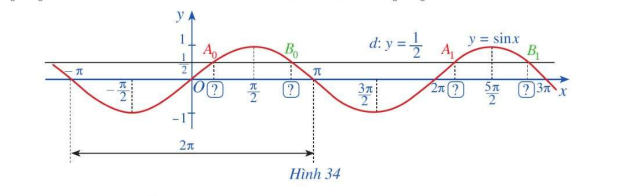
b)     Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \sin x,x \in \left[ {\pi ;3\pi } \right]\) tại hai giao điểm \({A_1},{B_1}\) (Hình 34). Tìm hoành độ của hai giao điểm \({A_1},{B_1}\).

Bài 17 :

Giải phương trình được nêu trong bài toán mở đầu.

Bài 18 :

a) Giải phương trình \(\cos x =  - \frac{1}{2}\)

b) Tìm góc lượng giác x sao cho \(\cos x = \cos \left( { - {{87}^ \circ }} \right)\)

Bài 19 :

a)     Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \cos x,x \in \left[ { - \pi ;\pi } \right]\) tại hai giao điểm \({C_0},{D_0}\) (Hình 35). Tìm hoành độ giao điểm của hai giao điểm \({C_0},{D_0}\).

b)     Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \cos x,x \in \left[ {\pi ;3\pi } \right]\) tại hai giao điểm \({C_1},{D_1}\) (Hình 35). Tìm hoành độ giao điểm của hai giao điểm \({C_1},{D_1}\).

Bài 20 :

a) Giải phương trình \(\tan x = 0\).

b) Tìm góc lượng giác x saoo cho \(\tan x = \tan {67^ \circ }\).

Bài 21 :

Quan sát giao điểm của đồ thị hàm số y = tan x và đường thẳng y = 1

a)     Từ hoành độ giao điểm của đồ thị hàm số y = tanx và đường thẳng y = m trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó

b)     Có nhận xét gì về nghiệm của phương trình tanx = 1

Bài 22 :

a) Giải phương trình \(\cot x = 1\)

b) Tìm góc lượng giác x sao cho \(\cot x = \cot \left( { - {{83}^ \circ }} \right)\)

Bài 23 :

Quan sát các giao điểm của đồ thị hàm số y = cotx và đường thẳng y = -1 (Hình 37)

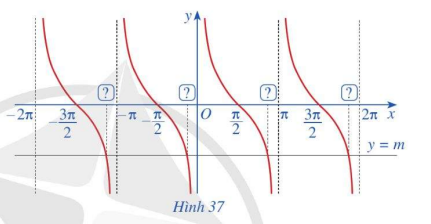
a)     Từ hoành độ giao điểm của đồ thị hàm số y = cotx và đường thẳng y = m trên khoảng \(\left( {0;\pi } \right)\), hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó.

b)     Có nhận xét gì về nghiệm của phương trình cotx = -1?

Bài 24 :

Giải phương trình:

a)     \(\sin \left( {2x - \frac{\pi }{3}} \right) =  - \frac{{\sqrt 3 }}{2}\)

b)     \(\sin \left( {3x + \frac{\pi }{4}} \right) =  - \frac{1}{2}\)

c)     \(\cos \left( {\frac{x}{2} + \frac{\pi }{4}} \right) = \frac{{\sqrt 3 }}{2}\)

d)     \(2\cos 3x + 5 = 3\)

e)     \(3\tan x =  - \sqrt 3 \)

g)      \(\cot x - 3 = \sqrt 3 \left( {1 - \cot x} \right)\)

Bài 25 :

Giải phương trình

a)     \(\sin \left( {2x + \frac{\pi }{4}} \right) = \sin x\)

b)     \(\sin 2x = \cos 3x\)

c)     \({\cos ^2}2x = {\cos ^2}\left( {x + \frac{\pi }{6}} \right)\)

Bài 26 :

Số nghiệm của phương trình cosx = 0 trên đoạn \(\left[ {0;10\pi } \right]\) là

A.5

B.9

C.10

D.11

Bài 27 :

Số nghiệm của phương trình sinx = 0 trên đoạn \(\left[ {0;10\pi } \right]\) là:

A.10

B.6

C.5

D.11

Bài 28 :

Số nghiệm của phương trình \(\sin \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\) trên đoạn \(\left[ {0;\pi } \right]\) là:

A.4

B.1

C.2

D.3

Bài 29 :

Nghiệm âm lớn nhất của phương trình lượng giác \(cos2x = cos\left( {x + \frac{\pi }{3}} \right)\) là:

\(\begin{array}{l}A. - \frac{\pi }{9}\\B. - \frac{{5\pi }}{3}\\C. - \frac{{7\pi }}{9}\\D. - \frac{{13\pi }}{9}\end{array}\)

Bài 30 :

Số nghiệm của phương trình \(tanx = 3\) trong khoảng \(\left( { - \frac{\pi }{2};\frac{{7\pi }}{3}} \right)\) là

A. 1

B. 2

C. 3

D. 4