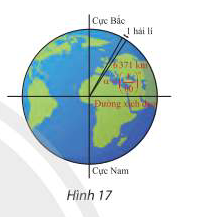
Hải lí là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc \(\alpha = {\left( {\frac{1}{{60}}} \right)^\circ }\) của đường kinh tuyến (Hình 17). Đổi số đo \(\alpha \) sang radian và cho biết 1 hải lí bằng khoảng bao nhiêu kilomet, biết bán kính trung bình của Trái Đất là 6371km. Làm tròn kết quả đến hàng phần trăm.
Sử dụng công thức đổi độ sang rad : \({\alpha ^ \circ } = \frac{{\pi \alpha }}{{180}}\,\)rad
Và công thức tính chiều dài cung tròn \(l = \frac{{\pi R{n^ \circ }}}{{{{180}^ \circ }}}\) với R là bán kính và \({n^ \circ }\)là số đo góc của cung tròn
Ta có \(\alpha = {\left( {\frac{1}{{60}}} \right)^\circ }\) suy ra \(\alpha = \frac{{\left( {\pi \frac{1}{{60}}} \right)}}{{180}} = \frac{\pi }{{10800}}\)
Một hải lí có độ dài bằng
\(l = \frac{{\pi R{n^ \circ }}}{{{{180}^ \circ }}} = \frac{{\pi .6371.{{\left( {\frac{1}{{60}}} \right)}^\circ }}}{{{{180}^ \circ }}} \approx 1,85\)(km)
Các bài tập cùng chuyên đề
Bài 1 :
Đổi số đo của góc \({70^0}\) sang đơn vị radian.
-
A.
\(\dfrac{{70}}{\pi }.\)
-
B.
\(\dfrac{7}{{18}}.\)
-
C.
\(\dfrac{{7\pi }}{{18}}.\)
-
D.
\(\dfrac{7}{{18\pi }}.\)
Bài 2 :
Đổi số đo của góc \( - \dfrac{{3\pi }}{{16}}{\rm{ rad}}\) sang đơn vị độ, phút, giây.
-
A.
\({33^0}45'.\)
-
B.
\( - {29^0}30'.\)
-
C.
\( - {33^0}45'.\)
-
D.
\( - {32^0}55.\)
Bài 3 :
Góc có số đo ${108^{\rm{o}}}$ đổi ra radian là
-
A.
$\dfrac{{3\pi }}{5}.$
-
B.
$\dfrac{\pi }{{10}}.$
-
C.
$\dfrac{{3\pi }}{2}.$
-
D.
$\dfrac{\pi }{4}.$
Bài 4 :
Góc có số đo \({120^{\rm{o}}}\) đổi sang rađian là góc
-
A.
\(\dfrac{\pi }{{10}}.\)
-
B.
\(\dfrac{{3\pi }}{2}.\)
-
C.
\(\dfrac{\pi }{4}.\)
-
D.
\(\dfrac{{2\pi }}{3}.\)
Bài 5 :
Góc có số đo \({120^o}\) đổi sang radian là:
-
A.
\(\dfrac{{3\pi }}{2}\).
-
B.
\(\dfrac{{2\pi }}{3}\).
-
C.
\(\dfrac{\pi }{4}\).
-
D.
\(\dfrac{\pi }{{10}}\).
Bài 6 :
Góc \(\dfrac{{5\pi }}{6}\) có số đo theo độ là
-
A.
\({112^o}50'\)
-
B.
\( - {150^o}\)
-
C.
\({120^o}\)
-
D.
\({150^o}\)
Bài 7 :
Cung có số đo 2250 được đổi sang số đo rad là :-
A.
\(225\pi \)
-
B.
\(\dfrac{{3\pi }}{4}\)
-
C.
\(\dfrac{{5\pi }}{4}\).
-
D.
\(\dfrac{{4\pi }}{3}\)
Bài 8 :
Góc \(\dfrac{{7\pi }}{6}\) có số đo bằng độ là:-
A.
\({30^o}\)
-
B.
\({105^o}\)
-
C.
\({150^o}\)
-
D.
\({210^o}\)
Bài 9 :
Công thức nào sau đây là đúng về mối quan hệ giữa độ và rad?
-
A.
\({1^o} = \frac{\pi }{{360}}\) rad
-
B.
\({1^o} = \frac{\pi }{{180}}\) rad
-
C.
1 rad\( = - {\left( {\frac{{90}}{\pi }} \right)^o}\)
-
D.
1 rad\( = {\left( {\frac{{90}}{\pi }} \right)^o}\)
Bài 10 :
Một đu quay ở công viên có bán kính bằng 10 m. Tốc độ của đu quay là 3 vòng/phút. Hỏi mất bao lâu để đu quay được góc \(270^o\) ?
-
A.
\(\frac{2}{3}\) phút
-
B.
\(\frac{1}{3}\) phút
-
C.
\(\frac{1}{4}\) phút
-
D.
\(\frac{1}{2}\) phút
Bài 11 :
a) Đổi từ độ sang rađian các số đo sau: \({360^ \circ }, - {450^ \circ }\)
b) Đổi từ rađian sang độ các số đo sau: \(3\pi , - \frac{{11\pi }}{5}\)
Bài 12 :
Hoàn thành bảng sau:
Bài 13 :
Hoàn thành bảng chuyển đổi đơn vị đo của các góc sau đây:
|
Số đo theo độ |
0° |
? |
45° |
60° |
? |
120° |
? |
150° |
180° |
|
Số đo theo rad |
? |
\(\frac{\pi }{6}(rad)\) |
? |
? |
\(\frac{\pi }{2}(rad)\) |
? |
\(\frac{{3\pi }}{4}(rad)\) |
? |
\(\pi (rad)\) |
Bài 14 :
Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung AB có độ dài đúng bằng R (Hình 9). Đo và cho biết \(\widehat {AOB}\) có số đo bằng bao nhiêu độ.
Bài 15 :
Đổi số đo của các góc sau đây sang radian
a) \(38^\circ \)
b) \( - 115^\circ \)
c) \({\left( {\frac{3}{\pi }} \right)^\circ }\)
Bài 16 :
Đổi số đo của các góc sau đây sang độ:
a) \(\frac{\pi }{{12}}\)
b) -5
c) \(\frac{{13\pi }}{9}\)
Bài 17 :
Góc có số đo \({75^o}\) bằng bao nhiêu radian?
-
A.
\(\frac{{5\pi }}{{12}}\)
-
B.
\(\frac{{7\pi }}{{12}}\)
-
C.
\(\frac{\pi }{2}\)
-
D.
\(\frac{\pi }{6}\)
Bài 18 :
Góc có số đo \(\frac{\pi }{6}\) radian bằng bao nhiêu độ?
-
A.
\({30^o}\)
-
B.
\({45^o}\)
-
C.
\({60^o}\)
-
D.
\({90^o}\)
Bài 19 :
Nếu một góc lượng giác có số đo là \(\alpha = - {45^{\rm{o}}}\) thì số đo radian của nó là
-
A.
\( - \frac{\pi }{2}\)
-
B.
\( - \frac{\pi }{4}\)
-
C.
\(\frac{\pi }{4}\)
-
D.
\(\frac{\pi }{2}\)
Bài 20 :
Khẳng định nào sau đây là đúng?
-
A.
\(\pi \) rad = \({1^o}\)
-
B.
\(\pi \) rad = \({60^o}\)
-
C.
\(\pi \) rad = \({180^o}\)
-
D.
\(\pi \) rad = \({120^o}\)
Bài 21 :
Đổi số đo của góc \( - \frac{{3\pi }}{{16}}\) rad sang đơn vị độ, phút, giây.
-
A.
33°45'
-
B.
−29°30'
-
C.
−33°45'
-
D.
−32°55'
Bài 22 :
Đổi số đo của góc $\alpha = 30^\circ $ sang rađian.
-
A.
\(\alpha = \frac{\pi }{2}\)
-
B.
\(\alpha = \frac{\pi }{4}\)
-
C.
\(\alpha = \frac{\pi }{6}\)
-
D.
\(\alpha = \frac{\pi }{3}\)
Bài 23 :
Hoàn thành bảng sau
Bài 24 :
Đổi số đo góc \(\alpha = {105^0}\) sang rađian ta được:
A.\(\alpha = \frac{{5\pi }}{8}\).
B. \(\alpha = \frac{\pi }{8}\).
C. \(\alpha = \frac{{7\pi }}{{12}}\).
D. \(\alpha = \frac{{9\pi }}{{12}}\).
Bài 25 :
Góc có số đo \(\frac{{7\pi }}{4}\) radian bằng bao nhiêu độ?
-
A.
\({315^o}\)
-
B.
\({45^o}\)
-
C.
\({345^o}\)
-
D.
\({275^o}\)
Bài 26 :
Đổi số đo của các góc sau đây sang radian:
a) \({15^0}\);
b) \({65^0}\);
c) \( - {105^0}\);
d) \({\left( {\frac{{ - 5}}{\pi }} \right)^0}\).
Bài 27 :
Đổi số đo của các góc sau đây sang độ:
a) 6;
b) \(\frac{{4\pi }}{{15}}\);
c) \( - \frac{{19\pi }}{8}\);
d) \(\frac{5}{3}\).
Bài 28 :
Đổi từ rađian sang độ với số đo $ - \frac{{13\pi }}{5}$ ta được
-
A.
$36^\circ $.
-
B.
$468^\circ $.
-
C.
$ - 468^\circ .$
-
D.
$486^\circ $.
