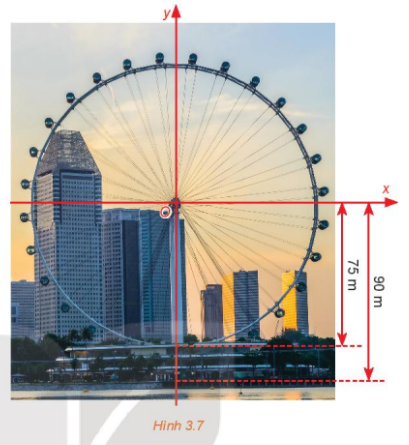
Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét?
Bước 1: Giả sử chiều quay của chiếc đu quay. Xác định vị trí của cabin sau 20 phút.
Bước 2: Dựa vào giá trị lượng giác của góc, xác định khoảng cách từ cabin đến Ox (trong hình H.3.7)
Bước 3: Suy ra độ cao của người đó sau 20 phút quay.
Giả sử chiếc đu quay quay theo chiều kim đồng hồ.
Gọi M là vị trí của cabin, M’ là vị trí của cabin sau 20 phút và các điểm A A’, B, H như hình dưới.
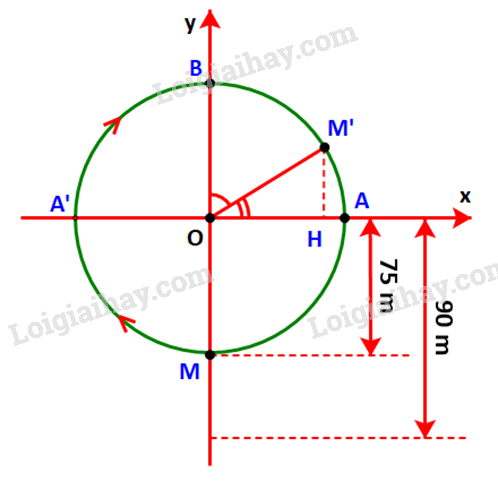
Vì đi cả vòng quay mất 30 phút nên sau 15 phút đầu tiên, cabin đi chuyển từ điểm M đến điểm B, được \(\frac{1}{2}\) chu vi đường tròn.
Trong 5 phút tiếp theo, cabin đi chuyển từ điểm B đến điểm M’ tương ứng \(\frac{1}{6}\) chu vi đường tròn (do đi cả vòng hết 30 phút) hay \(\frac{1}{3}\) cung BM.
Do đó: \(\widehat {BOM'} = \frac{1}{3}{.180^o} = {60^o}\)\( \Rightarrow \widehat {AOM'} = {90^o} - {60^o} = {30^o}.\)
\( \Rightarrow M'H = \sin {30^o}.OM' = \frac{1}{2}.75 = 37,5\left( m \right).\)
\( \Rightarrow \) Độ cao của người đó là: 37,5 + 90 = 127,5 (m).
Vậy sau 20 phút quay người đó ở độ cao 127,5 m.
Chuyển động tròn và tính chu kỳ
Khi một vật thể chuyển động trên một quỹ đạo tròn đều, nó sẽ hoàn thành một vòng quay trong một khoảng thời gian nhất định, gọi là chu kỳ. Trong một chu kỳ, vật thể quay được một góc là 360 độ (hoặc $2\pi$ radian). Tỷ lệ thời gian quay so với chu kỳ sẽ tương ứng với tỷ lệ góc quay so với 360 độ.
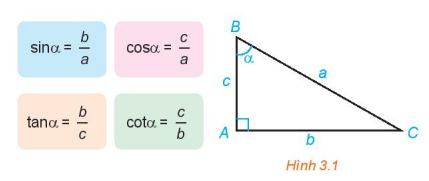
Giá trị lượng giác trong tam giác vuông
Trong một tam giác vuông, các tỉ số lượng giác (sin, cos, tan, cot) liên hệ giữa các cạnh và các góc nhọn của tam giác. Cụ thể, hàm sin của một góc trong tam giác vuông được định nghĩa là tỷ số giữa cạnh đối diện với góc đó và cạnh huyền.

Các bài tập cùng chuyên đề
Bài 1 :
Trong Hình 3.6, hai điểm M, N ứng với hai góc phụ nhau \(\alpha \) và \({90^o} - \alpha \) (\(\widehat {xOM} = \alpha ,\;\;\widehat {xON} = {90^o} - \alpha \)). Chứng mình rằng \(\Delta MOP = \Delta NOQ\). Từ đó nêu mối quan hệ giữa \(\cos \alpha \) và \(\sin \left( {{{90}^o} - \alpha } \right)\).
Bài 2 :
Nêu nhận xét về vị trí của hai điểm M, M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa \(\sin \alpha \) và \(\sin \left( {{{180}^o} - \alpha } \right)\), giữa \(\cos \alpha \) và \(\cos \left( {{{180}^o} - \alpha } \right)\).
Bài 3 :
b) \(2\sin \left( {{{180}^o} - \alpha } \right).\cot \alpha - \cos \left( {{{180}^o} - \alpha } \right).\tan \alpha .\cot \left( {{{180}^o} - \alpha } \right)\) với \({0^o} < \alpha < {90^o}\).
Bài 4 :
a) \(\sin {100^o} + \sin {80^o} + \cos {16^o} + \cos {164^o};\)
Bài 5 :
Bạn đã biết tỉ số lượng giác của một góc nhọn. Đối với góc tù thì sao?
Bài 6 :
Bạn đã biết tỉ số lượng giác của một góc nhọn. Đối với góc tù thì sao?
Bài 7 :
Trên nửa đường tròn đơn vị ta có dây cung MN song song với trục Ox và \(\widehat {xOM} = \alpha \).
a) Chứng minh \(\widehat {xON} = {180^o} - \alpha \)
b) Biểu diễn giá trị lượng giác của góc \({180^o} - \alpha \) theo giá trị lượng giác của góc \(\alpha \).
Bài 8 :
Cho biết \(\sin \alpha = \frac{1}{2},\) tìm góc \(\alpha \;({0^o} \le \alpha \le {180^o})\) bằng cách vẽ nửa đường tròn đơn vị.
Bài 9 :
Tính các giá trị lượng giác: \(\sin {120^o};\cos {150^o};\cot {135^o}.\)
Bài 10 :
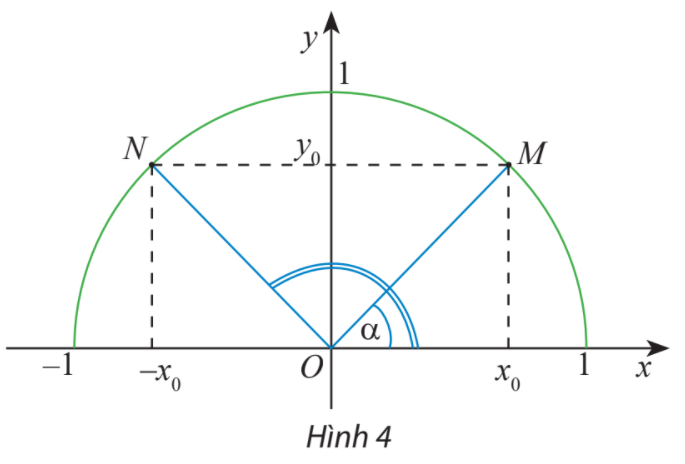
Trên nửa đường tròn đơn vị, cho dây cung NM song song với trục Ox (Hình 4). Tính tổng số đo của hai góc \(\widehat {xOM}\) và \(\widehat {xON}.\)
Bài 11 :
Cho biết \(\sin {30^o} = \frac{1}{2};\sin {60^o} = \frac{{\sqrt 3 }}{2};\tan {45^o} = 1.\) Sử dụng mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau, phụ nhau để tính giá trị của \(E = 2\cos {30^o} + \sin {150^o} + \tan {135^o}.\)
Bài 12 :
Chứng minh các hệ thức sau:
a) \(\sin {20^o} = \sin {160^o}\)
b) \(\cos {50^o} = - \cos {130^o}\)
Bài 13 :
Cho tam giác ABC. Chứng minh rằng:
a) \(\sin A = \sin \;(B + C)\)
b) \(\cos A = - \cos \;(B + C)\)
Bài 14 :
Trong các đẳng thức sau, đẳng thức nào đúng?
-
A.
\(\sin ({180^o} - \alpha ) = - \cos \alpha \)
-
B.
\(\sin ({180^o} - \alpha ) = - \sin \alpha \)
-
C.
\(\sin ({180^o} - \alpha ) = \cos \alpha \)
-
D.
\(\sin ({180^o} - \alpha ) = \sin \alpha \)
Bài 15 :
Trong các đẳng thức sau, đẳng thức nào đúng?
-
A.
\(\sin ({90^o} - \alpha ) = - \cos \alpha \)
-
B.
\(\sin ({90^o} - \alpha ) = - \sin \alpha \)
-
C.
\(\sin ({90^o} - \alpha ) = \cos \alpha \)
-
D.
\(\sin ({90^o} - \alpha ) = \sin \alpha \)
Bài 16 :
Trong các đẳng thức sau, đẳng thức nào đúng?
-
A.
\(\sin ({180^o} - \alpha ) = - \sin \alpha \)
-
B.
\(\cos ({180^o} - \alpha ) = \cos \alpha \)
-
C.
\(\sin ({90^o} - \alpha ) = \cos \alpha \)
-
D.
\(\sin ({90^o} - \alpha ) = \sin \alpha \)
Bài 17 :
Khẳng định nào sau đây là đúng?
A. \(\sin \alpha = \sin \left( {180^\circ - \alpha } \right)\)
B. \(\cos \alpha = \cos \left( {180^\circ - \alpha } \right)\)
C. \(\tan \alpha = \tan \left( {180^\circ - \alpha } \right)\)
D. \(\cot \alpha = \cot \left( {180^\circ - \alpha } \right)\)
Bài 18 :
Cho 00 < \(\alpha \), \(\beta \) < 1800 và \(\alpha + \beta = {180^0}\). Chọn câu trả lời sai
A. \(\sin \alpha + \sin \beta = 0\)
B. \(\cos \alpha + \cos \beta = 0\)
C. \(\tan \alpha + \tan \beta = 0\)
D. \(\cot \alpha + \cot \beta = 0\)
Bài 19 :
Mệnh đề nào sau đây đúng?
-
A.
sin (180° – α) = – sin α
-
B.
cos (180° – α) = – cos α
-
C.
tan (180° – α) = tan α
-
D.
cot (180° – α) = cot α
Bài 20 :
Trong các khẳng định sau, khẳng định nào sai?
-
A.
\(\sin {30^o} = - \sin {150^o}\)
-
B.
\(\tan {30^o} = - \tan {150^o}\)
-
C.
\(\cot {30^o} = - \cot {150^o}\)
-
D.
\(\cos {30^o} = - \cos {150^o}\)