Biểu thức \({x^2} - x + \frac{1}{4}\) được viết dưới dạng bình phương của một hiệu:
A. \({\left( {x-1} \right)^2}\).
B. \({\left( {x - \frac{1}{2}} \right)^2}\).
C. \({\left( {2x - \frac{1}{2}} \right)^2}\).
D. \({\left( {\frac{1}{2}x - 1} \right)^2}\).
Sử dụng hằng đẳng thức bình phương của một hiệu: \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\).
Ta có:
\({x^2} - x + \frac{1}{4} = {x^2} - 2.\frac{1}{2}.x + {\left( {\frac{1}{2}} \right)^2} = {\left( {x - \frac{1}{2}} \right)^2}.\)
=> Chọn đáp án B.

Các bài tập cùng chuyên đề
Bài 1 :
Với hai số a, b bất kì, viết \(a - b = a + \left( { - b} \right)\) và áp dụng hằng đẳng thức bình phương của một tổng để tính \({\left( {a - b} \right)^2}\).
Bài 2 :
Khai triển \({\left( {3x - 2y} \right)^2}\)
Bài 3 :
Trong trò chơi “Ai thông minh hơn học sinh lớp 8”, người dẫn chương trình yêu cầu các bạn học sinh cho biết kết quả của phép tính \({1002^2}\). Chỉ vài giây sau, Nam đã tính ra kết quả chính xác và giành được điểm. Em hãy giải thích xem Nam đã tính nhanh như thế nào.
Bài 4 :
Tính nhanh: \({49^2}\)
Bài 5 :
Tính:
a) \({\left( {3a - 1} \right)^2}\)
b) \({\left( {4u - 5v} \right)^2}\)
Bài 6 :
Viết các biểu thức sau dưới dạng bình phương của một hiệu:
a) \({a^2} - 12a + 36\);
b) \(25{x^2} + 64{y^2} - 80xy\)
Bài 7 :
Trong Hình 1.9, diện tích của hình vuông là \(9m - 42m + 49\), với \(m > 3\).
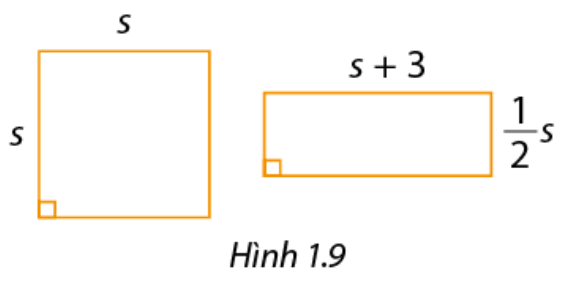
a) Tìm độ dài cạnh hình vuông theo \(m\). Từ đó biểu diễn \(s\)theo \(m\).
b) Tính diện tích hình chữ nhật trong hình 1.9 theo \(m\).
Bài 8 :
Kết quả của khai triển phép tính \(\left( \frac{1}{2} x - 1\right)^2\) là
-
A.
\(\frac{1}{2}x^2 - \frac{1}{2}x + 1\)
-
B.
\(\frac{1}{4}x^2 - 1\)
-
C.
\(\frac{1}{4}x^2 - \frac{1}{2}x + 1\)
-
D.
\(\frac{1}{4}x^2 - x + 1\)
Bài 9 :
-
A.
10.
-
B.
-10
-
C.
5.
-
D.
-5.
Bài 10 :
Cho biểu thức \(A = \frac{{16}}{{{x^2} - 2x + 5}}\). Tính giá trị lớn nhất của biểu thức A.
Bài 11 :
Viết biểu thức \(25{x^2} - 20xy + 4{y^2}\) dưới dạng bình phương của một hiệu.
-
A.
\({\left( {5x + 2y} \right)^2}\).
-
B.
\({\left( {2x - 5y} \right)^2}\).
-
C.
\({\left( {25x - 4y} \right)^2}\).
-
D.
\({\left( {5x - 2y} \right)^2}\).
Bài 12 :
Kết quả của biểu thức \({\left( {x + 2} \right)^2} - 4\left( {x + 2} \right) + 4\) là
-
A.
\({x^2} + 16\).
-
B.
\({x^2} + 8x + 16\).
-
C.
\({x^2} - 4x\).
-
D.
\({x^2}\).
Bài 13 :
Tìm giá trị nhỏ nhất của phân thức \(\frac{{12}}{{12 - 4x - {x^2}}}\).
Bài 14 :
Khai triển hằng đẳng thức \({\left( {2x - 3} \right)^2}\), ta được
-
A.
\(4{x^2} - 12x + 9\).
-
B.
\(4{x^2} - 6x + 9\).
-
C.
\(2{x^2} - 6x + 3\).
-
D.
\(4{x^2} + 12x + 9\).
Bài 15 :
Kết quả khai triển \({\left( {2x - 1} \right)^2}\) là:
-
A.
\(4{x^2} + 4x + 1\).
-
B.
\(2{x^2} - 4x + 1\).
-
C.
\(4{x^2} - 4x - 1\).
-
D.
\(4{x^2} - 4x + 1\).
Bài 16 :
Dùng hằng đẳng thức đáng nhớ biến đổi biểu thức \({\left( {x - 2y} \right)^2}\) ta được kết quả là:
-
A.
\({x^2} - 2xy + 4{y^2}\).
-
B.
\({x^2} - 4xy + 2{y^2}\).
-
C.
\({x^2} - 4xy + 4{y^2}\).
-
D.
\({x^2} - 4{y^2}\).
Bài 17 :
Kết quả của phép tính \({72^2} + {22^2} - 44.72\) là:
-
A.
784.
-
B.
250.
-
C.
2500.
-
D.
8836.
Bài 18 :
Bác An cắt một sợi dây thép dài $30cm$ thành hai đoạn. Mỗi đoạn được uốn thành một hình vuông. Bác An căng vải trên hai khung đó. Hỏi cần cắt đoạn dây như thế nào để tổng diện tích phần vải căng đạt giá trị nhỏ nhất (coi mép vải thừa không đáng kể).

















