Câu 4 trang 212 SGK Giải tích 12 Nâng caoHỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy để được lãi nhiều nhất? GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn Quảng cáo
Đề bài Một xưởng in có 8 máy in, mỗi máy in được 3600 bản in trong một giờ. Chi phí để vận hành một máy trong mỗi lần in là 50 nghìn đồng. Chi phí để n máy chạy trong một giờ là 10(6n + 10) nghìn đồng. Hỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy để được lãi nhiều nhất? Phương pháp giải - Xem chi tiết - Lập hàm số chi phí cần bỏ ra theo ẩn là số máy in sử dụng. - Số lãi có được nhiều nhất khi chi phí bỏ ra là ít nhất nên cần đi tìm GTNN của hàm số trên. Lời giải chi tiết Gọi x là số máy in được sử dụng (x nguyên, 1 ≤ x ≤ 8) Một giờ, mỗi máy in được 3600 bản nên x máy in được 3600x bản. Khi đó, thời gian in 50000 tờ quảng cáo là: \({{50000} \over {3600x}}\,(h) = {{125} \over {9x}}\,(h)\) Tổng chi phí để in 50000 tờ quảng cáo là: \(f(x) = {{125} \over {9x}}(6x + 10).10 + 50x\) (nghìn đồng) Số lãi sẽ nhiều nhất nếu chi phí ít nhất Ta cần tìm giá trị nhỏ nhất của f(x) trên [1, 8] Ta có: \(\eqalign{ Bảng biến thiên:
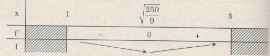
Trên [1, 8] đạt giá trị nhỏ nhất tại \(x = \sqrt {{{250} \over 9}} \) Vì \(x\) nguyên nên khi sử dụng 5 máy thì thì thu được nhiều lãi nhất. Chú ý: Trong bài toán này, vì số máy in chỉ thuộc từ 1 đến 8 nên các em có thể thay trực tiếp x=1,2,...,8 và hàm số và tìm GTNN. Loigiaihay.com
|