Trả lời câu hỏi 2 trang 33 SGK Giải tích 12Khảo sát sự biến thiên và vẽ đồ thị của hàm số ... GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn Quảng cáo
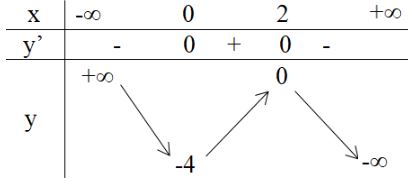
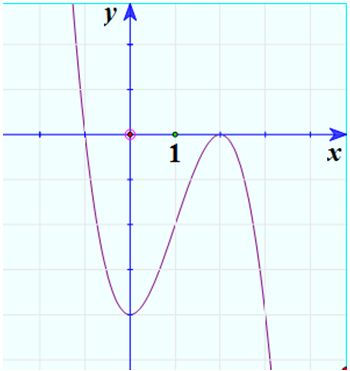
Đề bài Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = - {x^3}\; + {\rm{ }}3{x^2}\; - {\rm{ }}4\) Nêu nhận xét về đồ thị của hàm số này với đồ thị của hàm số khảo sát trong Ví dụ 1. Video hướng dẫn giải Phương pháp giải - Xem chi tiết B1: Tìm TXĐ B2: Bảng biến thiên - Xét chiều biến thiên +Tính \(y'\). + Tìm các điểm mà tại đó hàm số không xác định và nghiệm của \(y'=0\). + Xét dấu đạo hàm suy ra chiều biến thiên - Tìm cực trị - Tính các giới hạn,tiệm cận (nếu có). - Lập bảng biến thiên B3: Vẽ đồ thị Lời giải chi tiết TXĐ: \(D = \mathbb R.\) Sự biến thiên: \(\eqalign{ \(y’ = -3x^2 + 6x.\) Cho \(y’ = 0 ⇒ x = 0\) hoặc \(x = 2.\) Bảng biến thiên
Hàm số đồng biến trên khoảng \((0,2)\) Hàm số nghịch biến trên các khoảng \((-∞,0), (2,+ ∞).\) Hàm số đạt cực đại bằng 0 tại \(x = 2.\) Hàm số đạt cực tiểu bằng -4 tại \(x = 0.\) Vẽ đồ thị hàm số
Nhận xét: hai đồ thị đối xứng nhau qua \(Oy.\) Loigiaihay.com  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
|
