Lý thuyết hàm số mũ, hàm số lôgaritTổng hợp lý thuyết hàm số mũ và hàm số lôgarit ngắn gọn, dễ hiểu GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn Quảng cáo
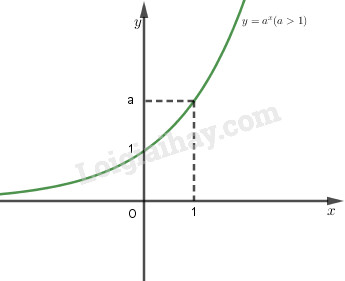
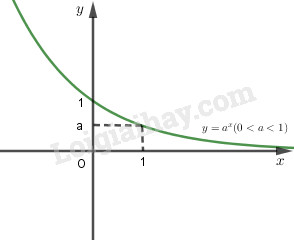
1. Định nghĩaHàm số mũ là hàm số có dạng \(y = {a^x}\), hàm số lôgarit là hàm số có dạng \(y = {\log _a}x\) ( với cơ số a dương khác 1). 2. Tính chất của hàm số mũ \(y = {a^x}\) \(( a > 0, a\ne 1)\).- Tập xác định: \(\mathbb{R}\). - Đạo hàm: \(∀x ∈\mathbb{R},y'= a^x \ln a\). - Chiều biến thiên +) Nếu \(a> 1\) thì hàm số luôn đồng biến +) Nếu \(0< a < 1\) thì hàm số luôn nghịch biến
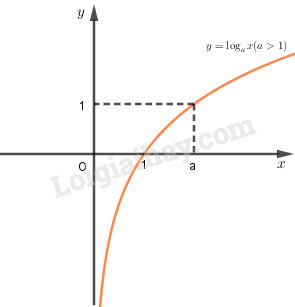
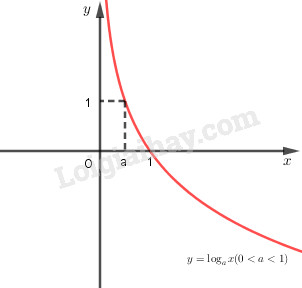
- Tiệm cận: trục \(Ox\) là tiệm cận ngang. - Đồ thị nằm hoàn toàn về phía trên trục hoành \((y = {a^x} >0 \, \forall x)\), và luôn cắt trục tung tại điểm \(( 0;1)\) và đi qua điểm \((1;a)\). 3. Tính chất của hàm số lôgarit \(y = {\log _a}x\) \((a> 0, a\ne1)\).- Tập xác định: \((0; +∞)\). - Đạo hàm \(∀x ∈ (0; +∞),y'= \dfrac{1}{x\ln a}\). - Chiều biến thiên: +) Nếu \(a> 1\) thì hàm số luôn đồng biến +) Nếu \(0< a < 1\) thì hàm số luôn nghịch biến - Tiệm cận: Trục \(Oy\) là tiệm cận đứng. - Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm \((1;0)\) và đi qua điểm \((a;1)\).
4. Chú ý- Nếu \(a > 1\) thì \(\ln a > 0\), suy ra \((a^x)'>0 \, \, \forall x\) và \({({\log_a}^x)}\; > 0,\;\;\forall x{\rm{ }} > 0;\) do đó hàm số mũ và hàm số lôgarit với cơ số lớn hơn 1 đều là những hàm số luôn luôn đồng biến. Tương tự, nếu \(0 < a< 1\) thì \(\ln a < 0\), \(({a^x})' < 0\) và \({({\log_a}^x)}\; < 0,\;\;\forall x{\rm{ }} > 0;\) ; hàm số mũ và hàm số lôgarit với cơ số nhỏ hơn 1 đều là những hàm số luôn luôn nghịch biến. - Công thức đạo hàm của hàm số lôgarit có thể mở rộng thành \( (\ln |x|)'= \dfrac{1}{x}, ∀x \ne 0\) và \((\log _a|x|)' = \frac{1}{{x\ln a}},{\rm{ }}\forall x \ne 0.\)
5. Bài tập về hàm số mũ, hàm số lôgaritBài 1. Chọn mệnh đề đúng: A. Hàm số \(y = {a^{ - x}}\left( {0 < a \ne 1} \right)\) đồng biến nếu \(a > 1\). B. Hàm số \(y = {a^{ - x}}\left( {0 < a \ne 1} \right)\) nghịch biến nếu \(0 < a < 1\). C. Hàm số \(y = {a^{ - x}}\left( {0 < a \ne 1} \right)\) đồng biến nếu \(0 < a < 1\). D. Hàm số \(y = {a^{ - x}}\left( {0 < a \ne 1} \right)\) luôn nghịch biến trên \(R\). Lời giải: Ta có: Hàm số $y=a^{-x}$ nghịch biến khi $a>1$ nên các đáp án B, D đều sai. \(y = {a^{ - x}} = \dfrac{1}{{{a^x}}} = {\left( {\dfrac{1}{a}} \right)^x}\left( {0 < a \ne 1} \right)\) nên hàm số đồng biến nếu \(\dfrac{1}{a} > 1 \Leftrightarrow 0 < a < 1\). Chọn đáp án C. Bài 2. Chọn mệnh đề đúng: A. Đồ thị hàm số \(y = {2^x}\) trùng với đồ thị hàm số \(y = {\left( {\dfrac{1}{2}} \right)^{ - x}}\) B. Đồ thị hàm số \(y = {2^x}\) trùng với đồ thị hàm số \(y = {2^{ - x}}\). C. Đồ thị hàm số \(y = {2^x}\) đối xứng với đồ thị hàm số \(y = {\left( {\dfrac{1}{2}} \right)^{ - x}}\) qua trục hoành D. Đồ thị hàm số \(y = {2^x}\) đối xứng với đồ thị hàm số \(y = {\left( {\dfrac{1}{2}} \right)^{ - x}}\) qua trục tung. Lời giải: Ta có: \(y = {\left( {\dfrac{1}{2}} \right)^{ - x}} = \dfrac{1}{{{{\left( {\dfrac{1}{2}} \right)}^x}}} = \dfrac{1}{{\dfrac{1}{{{2^x}}}}} = {2^x}\) nên hai hàm số \(y = {2^x}\) và \(y = {\left( {\dfrac{1}{2}} \right)^{ - x}}\) là một. Do đó chúng có chung đồ thị. Chọn đáp án A. Bài 3. Đồ thị hàm số dưới đây là của hàm số nào?
A. \(y = {2^{ - x}}\) B. \(y = {\left( {\dfrac{1}{2}} \right)^{ - x}}\) C. \(y = - {\left( {\dfrac{1}{2}} \right)^x}\) D. \(y = - {2^x}\) Lời giải: Quan sát đồ thị ta thấy nó nằm hoàn toàn phía dưới trục hoành nên loại A và B. Lại có, đồ thị hàm số đi qua điểm \(\left( { - 1; - 2} \right)\) nên thay tọa độ điểm này vào các hàm số C và D ta được đáp án C. Chọn đáp án C. Bài 4. Hàm số \(y = {2^{\ln x + {x^2}}}\) có đạo hàm là A. \(\left( {\dfrac{1}{x} + 2x} \right){2^{\ln x + {x^2}}}\) B. \(\left( {\dfrac{1}{x} + 2x} \right){2^{\ln x + {x^2}}}.\ln 2\) C. \(\dfrac{{{2^{\ln x + {x^2}}}}}{{\ln 2}}\) D. \(\left( {\dfrac{1}{x} + 2x} \right)\dfrac{{{2^{\ln x + {x^2}}}}}{{\ln 2}}\) Lời giải: Có $y = {2^{\ln x + {x^2}}} \Rightarrow y' = \left( {\dfrac{1}{x} + 2x} \right){2^{\ln x + {x^2}}}.\ln 2$ Chọn đáp án B. Bài 5. Gọi $(C)$ là đồ thị hàm số \(y = \log x\). Tìm khẳng định đúng? A. Đồ thị $(C)$ có tiệm cận đứng B. Đồ thị $(C)$ có tiệm cận ngang. C. Đồ thị $(C)$ cắt trục tung. D. Đồ thị $(C)$ không cắt trục hoành. Lời giải: - Đồ thị hàm số \(y = \log x\) nhận trục tung là tiệm cận đứng. - Đồ thị hàm số không có tiệm cận ngang và cắt trục hoành tại điểm $(1;0)$ nên các đáp án B,C,D đều sai Chọn đáp án A. Bài 6. Cho $a, b$ là các số thực, thỏa mãn \(0 < a < 1 < b\), khẳng định nào sau đây là đúng? A. \({\log _b}a + {\log _a}b < 0\) B. \({\log _b}a > 1\) C. \({\log _a}b > 0\) D. \({\log _a}b + {\log _b}a \ge 2\) Lời giải: Ta có: \(0 < a < 1\) nên hàm số \(y = {\log _a}x\) nghịch biến, do đó \(b > 1\) nên \({\log _a}b < {\log _a}1 = 0\). Vì \(b > 1\) nên hàm số \(y = {\log _b}x\) đồng biến, do đó \(a < 1\) nên \({\log _b}a < {\log _b}1 = 0\). Vậy \({\log _a}b < 0;{\log _b}a < 0 \Rightarrow {\log _a}b + {\log _b}a < 0\). Chọn đáp án A. Bài 7. Tìm tập xác định D của hàm số \(y = {\log _{\sqrt 2 }}\left( {\dfrac{{ - 3}}{{2 - 2x}}} \right)\). A. \(D = ( - \infty ;1)\) B. \(D = {\rm{[}}1; + \infty )\) C. \(D = ( - \infty ;1]\) D. \(D = (1; + \infty )\) Lời giải: Điều kiện : \(\dfrac{{ - 3}}{{2 - 2x}} > 0 \Leftrightarrow 2 - 2x < 0 \Leftrightarrow x > 1.\) Chọn đáp án D. Bài 8. Đạo hàm hàm số \(y = {\log _{2018}}\left( {2018x + 1} \right)\) là: A. \(\dfrac{1}{{x\ln 2018}}\) B. \(\dfrac{{2018}}{{2018\left( {x + 1} \right)\ln 2018}}\) C. \(\dfrac{1}{{\left( {2018x + 1} \right)\ln 2018}}\) D. \(\dfrac{{2018}}{{\left( {2018x + 1} \right)\ln 2018}}\) Lời giải: Ta có: \(\left[ {{{\log }_{2018}}\left( {2018x + 1} \right)} \right]' = \dfrac{{\left( {2018x + 1} \right)'}}{{\left( {2018x + 1} \right)\ln 2018}} = \dfrac{{2018}}{{\left( {2018x + 1} \right)\ln 2018}}\) Chọn đáp án D.
|