Bài 12 trang 124 SGK Hình học 12 Nâng cao

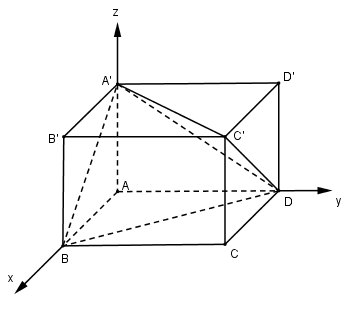
LG a

Tính khoảng cách từ điểm A tới mp(A’BD).

Lời giải chi tiết:

Chọn hệ trục tọa độ Oxyz như hình vẽ.

Ta có: \(A'\left( {0;0;c} \right),\,\,B\left( {a;0;0} \right),\,\,D\left( {0;b;0} \right).\)
Phương trình mặt phẳng (A’BD) là: \({x \over a} + {y \over b} + {z \over c} - 1 = 0.\)
Khoảng cách từ A(0; 0; 0) tới mp(A’BD) là:

\(d = {{\left| { - 1} \right|} \over {\sqrt {{1 \over {{a^2}}} + {1 \over {{b^2}}} + {1 \over {{c^2}}}} }} = {{abc} \over {\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}.\)

LG b

Tính khoảng cách từ điểm A’ tới đường thẳng C’D.

Lời giải chi tiết:

Ta có \(C'\left( {a;b;c} \right).\)

\(\eqalign{
& \overrightarrow {A'C'} = \left( {a,b,0} \right),\overrightarrow {C'D} = \left( { - a;0; - c} \right) \cr 
& \left[ {\overrightarrow {A'C'} ,\overrightarrow {C'D} } \right] = \left( { - bc,ac,ab} \right). \cr} \)

Khoảng cách từ \(A'\left( {0,0,c} \right)\) tới đường thẳng C’D là:

\({h_1} = {{\left| {\left[ {\overrightarrow {A'C'} ,\overrightarrow {C'D} } \right]} \right|} \over {\left| {\overrightarrow {C'D} } \right|}} = {{\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} } \over {\sqrt {{a^2} + {c^2}} }}.\)

LG c

Tính khoảng cách giữa hai đường thẳng BC’ và CD’.

Lời giải chi tiết:

Ta có \(\overrightarrow {BC'}  = \left( {0,b,c} \right),\overrightarrow {CD'}  = \left( { - a,0,c} \right),\) \(\overrightarrow {BC}  = \left( {0,b,0} \right).\)

Khoảng cách giữa BC’ và CD’ là:

\({h_2} = {{\left| {\left[ {\overrightarrow {BC'} ,\overrightarrow {CD'} } \right].\overrightarrow {BC} } \right|} \over {\left| {\left[ {\overrightarrow {BC'} ,\overrightarrow {CD'} } \right]} \right|}} = {{abc} \over {\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}.\)

Loigiaihay.com