Giải bài 5 trang 49 SGK Hình học lớp 12Từ một điểm M nằm nằm bên ngoài mặt cầu S( O; r) ta kẻ hai đường thẳng cắt mặt cầu lần lượt tại A, B và C, D. GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
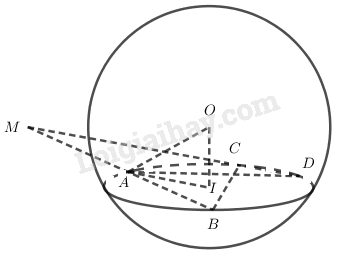
Từ một điểm \(M\) nằm nằm bên ngoài mặt cầu \(S( O; r)\) ta kẻ hai đường thẳng cắt mặt cầu lần lượt tại \(A, B\) và \(C, D\). LG a a) Chứng minh rằng \(MA.MB = MC.MD\). Phương pháp giải: +) Sử dụng các tam giác đồng dạng để chứng minh các tỉ lệ giữa các cạnh. Từ đó suy ra tích cần chứng minh. +) Sử dụng định lý Pi-ta-go và tỉ lệ vừa chứng minh ở câu a để tính đại lượng cần tính. Lời giải chi tiết:
Gọi \((P)\) là mặt phẳng chứa hai đường thẳng đã cho. Mặt phẳng\((P)\) cắt mặt cầu \(S(O;r)\) theo một đường tròn tâm \(I\), là hình chiếu vuông góc của \(O\) lên mặt phẳng \((P)\). Xét hai tam giác \(MAD\) và \(MCB\) có: +) \(\widehat B = \widehat D\) (Hai góc cùng chắn một cung) +) \(\widehat M\) chung \( \Rightarrow \Delta MAD\) đồng dạng với \(\Delta MCB.\) \(\Rightarrow{{MA} \over {MC}} = {{MD} \over {MB}}\) (các cặp cạnh tương ứng tỉ lệ). \(\Rightarrow MA.MB=MC.MD \, \, \, (dpcm)\) LG b b) Gọi \(MO = d\). Tính \(MA.MB\) theo \(r\) và \(d\). Phương pháp giải: +) Sử dụng các tam giác đồng dạng để chứng minh các tỉ lệ giữa các cạnh. Từ đó suy ra tích cần chứng minh. +) Sử dụng định lý Pi-ta-go và tỉ lệ vừa chứng minh ở câu a để tính đại lượng cần tính. Lời giải chi tiết: b) Đặt \(MO = d\), ta có \(OI\) vuông góc với \((P)\) và ta có: \(O{M^2} = M{I^2} = O{I^2};O{A^2} = O{I^2} + I{A^2}\) Hạ \(IH\) vuông góc \(AB\), ta có \(H\) là trung điểm của \(AB\). Ta có \(MA = MH - HA\); \(MB = MH + HB = MH + HA\). \(MA.MB = M{H^2} - H{A^2}\) \(= (M{H^2} + H{I^2}) - (H{A^2} + I{H^2})\) \( =M{I^2} - I{A^2} \) \(= (M{I^2} + O{I^2}) - (I{A^2} + O{I^2})\) \(= O{M^2} - O{A^2}\) \(= {d^2} - {r^2}\) Vậy \(MA.MB = {d^2} - {r^2}\). Loigiaihay.com  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
|
