Bài 7.12 trang 42 SGK Toán 11 tập 2 – Kết nối tri thức

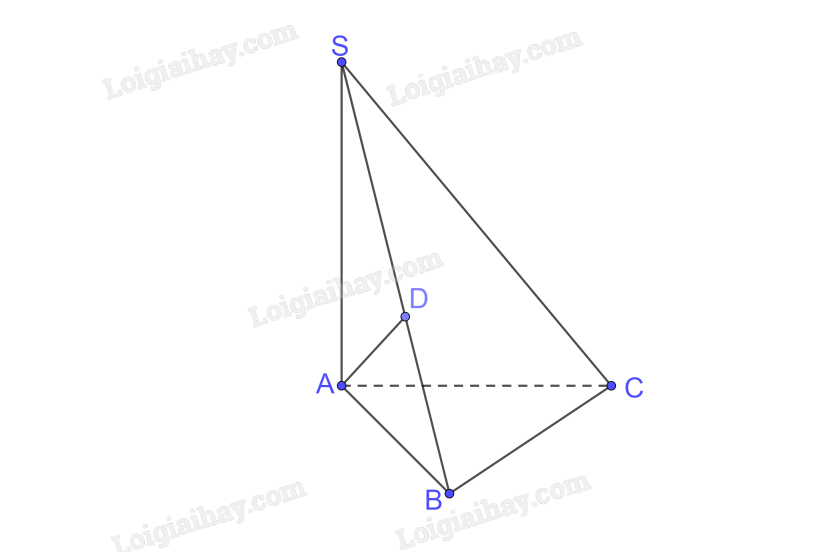
Đề bài

Cho hình chóp S.ABC có SA \( \bot \) (ABC), Tam giác ABC vuông tại B, SA=AB=BC=a 

a) Xác định hình chiếu của A trên mặt phẳng (SBC)

b) Tính góc giữa SC và mặt phẳng (ABC).

Lời giải chi tiết

 

a) Trong (SAB) kẻ \(AD \bot SB\) tại D.

Ta có: 

.\(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\\AB,SA \subset (SAB)\\AB \cap SA\end{array} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot AD\).

Ta có: 

\(\left\{ \begin{array}{l}AD \bot BC\\AD \bot SB\\BC,SB \subset (SBC)\\BC \cap SB\end{array} \right. \Rightarrow AD \bot (SBC)\). Suy ra D là hình chiếu của A trên (SBC).

b) A là hình chiếu của S trên (ABC) \(\left( {SA \bot \left( {ABC} \right)} \right)\)

C là hình chiếu của C trên (ABC)

\( \Rightarrow \) AC là hình chiếu của SC trên (ABC)

\( \Rightarrow \) \(\left( {SC,\left( {ABC} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)

Xét tam giác ABC vuông tại B có

\(A{C^2} = A{B^2} + B{C^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \)

Xét tam giác SAC vuông tại A có

\(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} \Rightarrow \widehat {SCA} = \arctan \frac{1}{{\sqrt 2 }}\)

Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = \arctan \frac{1}{{\sqrt 2 }}\)