Câu 24 trang 227 SGK Đại số và Giải tích 11 Nâng caoCho hyperbol (H) xác định bởi phương trình Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
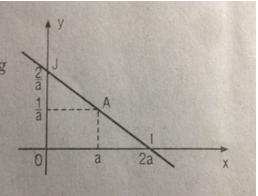
Cho hyperbol (H) xác định bởi phương trình \(y = {1 \over x}\) LG a Tìm phương trình tiếp tuyến (T) của (H) tại tiếp điểm A có hoành độ a (với a ≠ 0) Lời giải chi tiết:
Với mọi x ≠ 0, ta có : \(f'\left( x \right) = - {1 \over {{x^2}}}\) Phương trình tiếp tuyến (T) tại điểm \(A\left( {a;{1 \over a}} \right)\) là : \(y - {1 \over a}= - {1 \over {{a^2}}}\left( {x - a} \right)\) hay \(y = - {1 \over {{a^2}}}x + {2 \over a}\) LG b Giả sử (T) cắt trục Ox tại điểm I và cắt trục Oy tại điểm J. Chứng minh rằng A là trung điểm của đoạn thẳng IJ. Từ đó suy ra cách vẽ tiếp tuyến (T). Lời giải chi tiết: Tìm các giao điểm của (T) với hai trục tọa độ: Cho x=0 thì \(y={2 \over a}\). Cho y=0 thì x=2a. Do đó \(I\left( {2a;0} \right);\,J\left( {0;{2 \over a}} \right)\) Ta thấy: \[\left\{ \begin{array}{l} Nên \(A\left( {a;{1 \over a}} \right)\) là trung điểm của đoạn IJ. Từ đó suy ra cách vẽ tiếp tuyến (T) chính là đường thẳng IJ. Ta chỉ cần lấy hai điểm I, J có tọa độ như trên và nối lại sẽ được tiếp tuyến cần tìm. LG c Chứng minh rằng diện tích tam giác OIJ không phụ thuộc vào vị trí của điểm A. Lời giải chi tiết: Ta có: \[OI = \left| {2a} \right|,OJ = \left| {\frac{2}{a}} \right|\] Diện tích tam giác OIJ là : \(S = {1 \over 2}OI.OJ= {1 \over 2}\left| {2a.{2 \over a}} \right| = 2\) (đvdt) Vì S không phụ thuộc vào a nên diện tích tam giác OIJ không phụ thuộc vào vị trí của điểm A ϵ (H) Loigiaihay.com
|