Câu 32 trang 117 SGK Hình học 11 Nâng caoCho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = AA’ = a, AC’ = 2a. a. Tính khoảng cách từ điểm D đến mặt phẳng (ACD’) b. Tìm đường vuông góc chung của các đường thẳng AC’ và CD’. Tính khoảng cách giữa hai đường thẳng ấy. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = AA’ = a, AC’ = 2a. LG a Tính khoảng cách từ điểm D đến mặt phẳng (ACD’) Giải chi tiết:
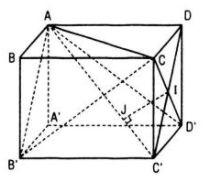
a. Xét tứ diện DACD’ có DA, DC, DD’ đôi một vuông góc nên khoảng cách DH từ D đến mặt phẳng (ACD’) được tính bởi hệ thức : \({1 \over {D{H^2}}} = {1 \over {D{A^2}}} + {1 \over {D{C^2}}} + {1 \over {DD{'^2}}}\) Ta có: DC = a. DD’ = a \(AC{'^2} = A{C^2} + CC{'^2} = D{A^2} + D{C^2} + CC{'^2}\) Hay \(4{a^2} = D{A^2} + {a^2} + {a^2},\)tức là \(D{A^2} = 2{a^2}\) Vậy \({1 \over {D{H^2}}} = {1 \over {2{a^2}}} + {1 \over {{a^2}}} + {1 \over {{a^2}}} = {5 \over {2{a^2}}}\) Do đó : \(DH = {{a\sqrt {10} } \over 5}\) LG b Tìm đường vuông góc chung của các đường thẳng AC’ và CD’. Tính khoảng cách giữa hai đường thẳng ấy. Giải chi tiết:
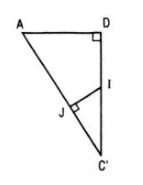
Vì CD = DD’ = a nên CD’ ⊥ C’D. Mặt khác AD ⊥ (CDD’C’) nên CD’ ⊥ AC’ và CD’ ⊥ mp(AC’D). Gọi giao điểm của CD’ với mp(AC’D) là I. Trong mp(AC’D) kẻ IJ vuông góc với AC’ tại J thì IJ là đường vuông góc chung của AC’ và CD’. Ta tính khoảng cách giữa AC’ và CD’ Ta có: ΔC’JI đồng dạng ΔC’DA nên \({{IJ} \over {AD}} = {{IC'} \over {AC'}}\) Suy ra : \(IJ = AD.{{C'D} \over {2AC'}}\) Mặt khác \(C'D = a\sqrt 2 \) nên \(IJ = a\sqrt 2 .{{a\sqrt 2 } \over {2.2a}} = {a \over 2}\) Loigiaihay.com
|