Bài 1.45 trang 22 SBT giải tích 12Giải bài 1.45 trang 22 sách bài tập giải tích 12. Giá trị lớn nhất của hàm số... GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn Quảng cáo
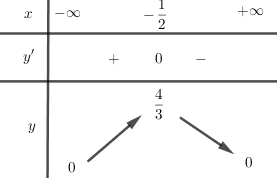
Đề bài Giá trị lớn nhất của hàm số \(y = \dfrac{1}{{{x^2} + x + 1}}\) trên khoảng \(\left( { - \infty ; + \infty } \right)\) là: A. \(1\) B. \(\dfrac{4}{3}\) C. \(\dfrac{5}{3}\) D. \(0\) Phương pháp giải - Xem chi tiết - Tính \(y'\), tìm nghiệm của \(y'=0\). - Lập bảng biến thiên của hàm số và kết luận. Lời giải chi tiết Ta có: \(y' = \dfrac{{ - 2x - 1}}{{{{\left( {{x^2} + x + 1} \right)}^2}}} = 0 \Leftrightarrow x = - \dfrac{1}{2}\). Bảng biến thiên:
Từ bảng biến thiên ta thấy, hàm số đạt GTLN \(\mathop {\max }\limits_{\left( { - \infty ; + \infty } \right)} y = \dfrac{4}{3}\) khi \(x = - \dfrac{1}{2}\). Chọn B. Loigiaihay.com  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
|
