Giải bài 4.32 trang 86 SGK Toán 7 tập 1 - Kết nối tri thứcCho tam giác MBC vuông tại M có B= 60°. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều. GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn Quảng cáo
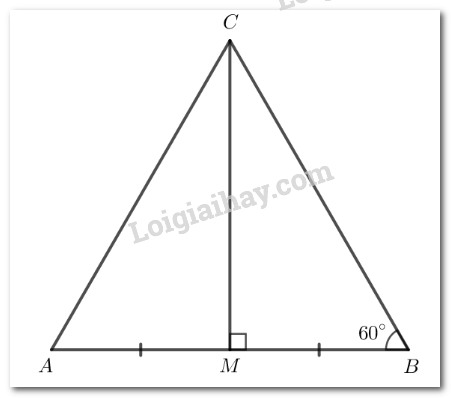
Đề bài Cho tam giác MBC vuông tại M có \(\widehat B\) = 60°. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều. Phương pháp giải - Xem chi tiết Chứng minh tam giác ABC cân tại C và có 1 góc bằng 60 độ. Lời giải chi tiết
Xét \(\Delta CMB\) và \(\Delta CMA\) có: MC chung \(\widehat{BMC}=\widehat{AMC}\) (= 90o) MB = MA (gt) Do đó \(\Delta CMB = \Delta CMA\) (c.g.c) Suy ra CA = CB (2 cạnh tương ứng). Nên tam giác ABC cân tại C. Mà \(\widehat B=\) 60o Vậy tam giác ABC đều.  Chia sẻ Bình luận
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
