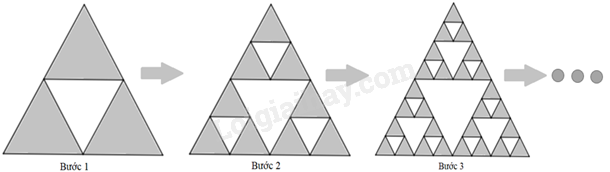
Giải bài 6 trang 94 sách bài tập toán 11 - Chân trời sáng tạo tập 1Từ một tam giác đều có diện tích bằng 1, ta thực hiện lần lượt các bước như sau: Bước 1: Nối trung điểm các cạnh của tam giác đã cho, chia tam giác này thành 4 tam giác nhỏ và bỏ đi tam giác ở giữa (bỏ đi 1 tam giác có diện tích \(\frac{1}{4}\)). Bước 2: Làm tương tự bước 1 với mỗi tam giác trong 3 tam giác còn lại (bỏ đi 3 tam giác, mỗi tam giác có diện tích \(\frac{1}{{{4^2}}}\)) Cứ tiếp tục quá trình như vậy (ở bước thứ n, bỏ đi \({3^{n - 1}}\) tam giác, mỗi tam giác có diện tích \(\frac{1 Quảng cáo
Đề bài Từ một tam giác đều có diện tích bằng 1, ta thực hiện lần lượt các bước như sau: Bước 1: Nối trung điểm các cạnh của tam giác đã cho, chia tam giác này thành 4 tam giác nhỏ và bỏ đi tam giác ở giữa (bỏ đi 1 tam giác có diện tích \(\frac{1}{4}\)). Bước 2: Làm tương tự bước 1 với mỗi tam giác trong 3 tam giác còn lại (bỏ đi 3 tam giác, mỗi tam giác có diện tích \(\frac{1}{{{4^2}}}\)) Cứ tiếp tục quá trình như vậy (ở bước thứ n, bỏ đi \({3^{n - 1}}\) tam giác, mỗi tam giác có diện tích \(\frac{1}{{{4^n}}}\)). Tính tổng diện tích các tam giác đã bỏ đi.
Phương pháp giải - Xem chi tiết Sử dụng kiến thức về tổng của cấp số nhân lùi vô hạn để tính: Cấp số nhân vô hạn \(\left( {{u_n}} \right)\) có công bội q thỏa mãn \(\left| q \right| < 1\) được gọi là cấp số nhân lùi vô hạn. Cấp số nhân lùi vô hạn này có tổng là: \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\) Lời giải chi tiết Tổng diện tích các tam giác đã bỏ đi là: \(S = \frac{1}{4} + 3.{\left( {\frac{1}{4}} \right)^2} + {3^2}.{\left( {\frac{1}{4}} \right)^3} + ... + {3^n}{\left( {\frac{1}{4}} \right)^{n + 1}} + ... = \frac{1}{4} + \frac{1}{4}.\frac{3}{4} + \frac{1}{4}.{\left( {\frac{3}{4}} \right)^2} + ... + \frac{1}{4}.{\left( {\frac{3}{4}} \right)^n} + ...\) Tổng trên là tổng của các số hạng lập thành một cấp số nhân lùi vô hạn với số hạng đầu \({u_1} = \frac{1}{4}\), công bội \(q = \frac{3}{4}\). Do đó, \(S = \frac{1}{4}.\frac{1}{{1 - \frac{3}{4}}} = 1\).
|