Giải Bài 8 trang 69 sách bài tập toán 7 - Cánh diềuCho tam giác ABC. Kẻ HB vuông góc với AC tại H. Kẻ CK vuông góc với AB tại K, BH cắt CK tại I (Hình 5). Nếu \(\widehat {{A^{}}} < {90^o}\) thì khi đó ta có: GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn Quảng cáo
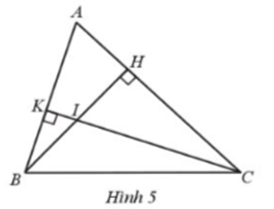
Đề bài Cho tam giác ABC. Kẻ HB vuông góc với AC tại H. Kẻ CK vuông góc với AB tại K, BH cắt CK tại I (Hình 5). Nếu \(\widehat {{A^{}}} < {90^o}\) thì khi đó ta có: A. \(\widehat {ABH} < \widehat {ACK}\) B. \(\widehat {ABH} = \widehat {ACK}\) C. \(\widehat {ABH} > \widehat {ACK}\) D. \(\widehat {ABH} = 90^\circ + \widehat {ACK}\) Phương pháp giải - Xem chi tiết Sử dụng tổng hai góc nhọn trong một tam giác vuông bằng \({90^o}\) để tìm ra đáp án. Lời giải chi tiết Đáp án đúng là: B • Xét ∆ABH vuông tại H ta có: \(\widehat {{A^{}}} + \widehat {ABH} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°). Suy ra \(\widehat {ABH} = 90^\circ - \hat A\) (1) • Xét ∆ACK vuông tại K ta có: \(\hat A + \widehat {ACK} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°). Suy ra \(\widehat {ACK} = 90^\circ - \hat A\)(2) Từ (1) và (2) ta có \(\widehat {ABH} = \widehat {ACK}\left( { = 90^\circ - \hat A} \right)\).  Chia sẻ Bình luận
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
