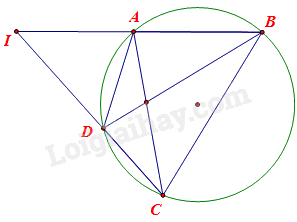
Giải bài tập 4 trang 79 SGK Toán 9 tập 2 - Cánh diều

Đề bài

Cho tứ giác nội tiếp ABCD có hai tia CD và BA cắt nhau tại I. Chứng minh:

a)\(\widehat {IAD} = \widehat {BCD}.\)

b) IA.IB = ID.IC.

Lời giải chi tiết

a) Do tứ giác ABCD nội tiếp đường tròn nên \(\widehat {DAB} + \widehat {DCB} = 180^\circ \).

Mà \(\widehat {DAB} + \widehat {IAD} = 180^\circ \) (kề bù)

Suy ra \(\widehat {DCB} = \widehat {IAD}\) hay \(\widehat {IAD} = \widehat {BCD}.\)

b) Xét tam giác IAD và tam giác ICB có:

\(\widehat I\) chung

\(\widehat {IAD} = \widehat {BCD}\) (cmt)

Nên \(\Delta IAD\backsim \Delta ICB\)(g.g)

Suy ra \(\frac{{IA}}{{ID}} = \frac{{IC}}{{IB}}\) hay IA.IB = IC.ID (đpcm).