Giải bài tập 7 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạoCho đường tròn (O) có hai đường kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung nhỏ AC rồi vẽ tiếp tuyến với đường tròn (O) tại M. Tiếp tuyến này cắt đường thẳng CD tại S. Chứng minh rằng (widehat {MSD} = 2widehat {MBA}). Quảng cáo
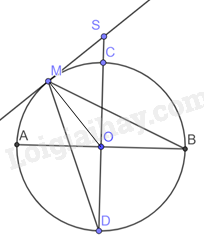
Đề bài Cho đường tròn (O) có hai đường kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung nhỏ AC rồi vẽ tiếp tuyến với đường tròn (O) tại M. Tiếp tuyến này cắt đường thẳng CD tại S. Chứng minh rằng \(\widehat {MSD} = 2\widehat {MBA}\). Video hướng dẫn giải Phương pháp giải - Xem chi tiết Đọc kĩ dữ liệu đề bài để vẽ hình. Chứng minh \(\widehat {MSD} = \widehat {MOA}\) và \(\widehat {MOA} = 2\widehat {MBA}\) suy ra \(\widehat {MSD} = 2\widehat {MBA}\) Lời giải chi tiết
Ta có SM \( \bot \) OM (Tính chất tiếp tuyến) Suy ra tam giác OSM vuông tại M Ta có \(\widehat {MSO} + \widehat {MOS} = {90^o}\) Và AB\( \bot \)CD (gt) Suy ra \(\widehat {MOS} + \widehat {MOA} = {90^o}\) Nên \(\widehat {MSO} = \widehat {MOA}\) hay \(\widehat {MSD} = \widehat {MOA}\) (1) Ta có \(\widehat {MOA} = 2\widehat {MBA}\) (góc ở tâm cùng chắn cung AM) (2) Từ (1) và (2) suy ra \(\widehat {MSD} = 2\widehat {MBA}\).
|