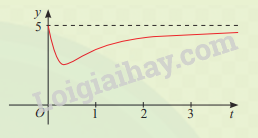
Giải câu hỏi mở đầu trang 14 SGK Toán 12 tập 1 - Chân trời sáng tạo

Đề bài

Sự phân huỷ của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hoà tan trong nước. Nồng độ oxygen (mg/l) trong một hồ nước sau t giờ (t \( \ge \) 0) khi một lượng rác thải hữu cơ bị xả vào hồ được xấp xỉ bởi hàm số (có đồ thị như đường màu đỏ ở hình bên):

\(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\)

Vào các thời điểm nào nồng độ oxygen trong nước cao nhất và thấp nhất?

(Theo: https://www.researchgate.net/publication/264903978_Microrespirometric_ characterization _of_activated_sludge_inhibition_by_copper_and_zinc)

 

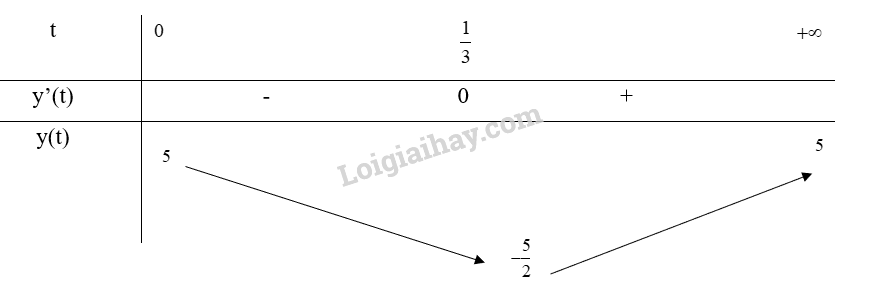
Lời giải chi tiết

Xét \(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\) trên nửa đoạn \([0; + \infty )\).

\(y'(t) = \frac{{135{t^2} - 15}}{{{{(9{t^2} + 1)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{1}{3}\\x =  - \frac{1}{3}(loai)\end{array} \right.\)

Bảng biến thiên:

Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[0; + \infty )} y(t) = y(\frac{1}{3}) =  - \frac{5}{2}\) và \(\mathop {\max }\limits_{[0; + \infty )} y(t) = y(0) = 5\).

Vậy vào các thời điểm t = 0 thì nồng độ oxygen trong nước cao nhất và t = \(\frac{1}{3}\) giờ thì nồng độ oxygen trong nước thấp nhất.