Giải mục 1 trang 61, 62 SGK Toán 10 tập 1 - Chân trời sáng tạo

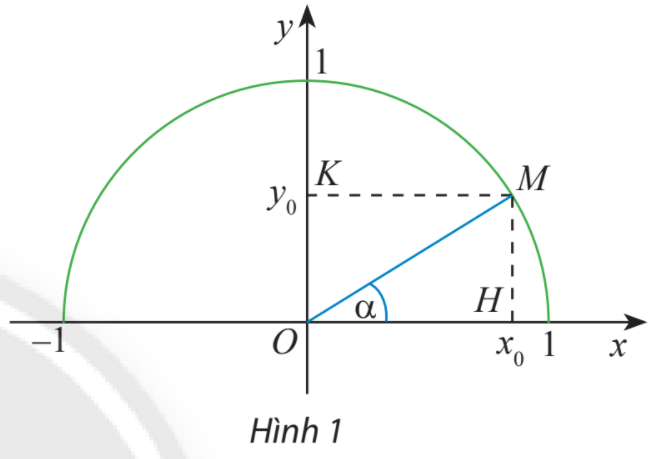
HĐ Khám phá 1

Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính \(R = 1\) nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn \(\alpha ,\)lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha .\) Giả sử điểm M có tọa độ \(({x_0};{y_0}).\) Trong tam giác vuông OHM, áp dụng cách tính các tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:

\(\sin \alpha  = {y_0};\;\cos \alpha  = {x_0};\;\tan \alpha  = \frac{{{y_0}}}{{{x_0}}};\;\cot \alpha  = \frac{{{x_0}}}{{{y_0}}}.\)

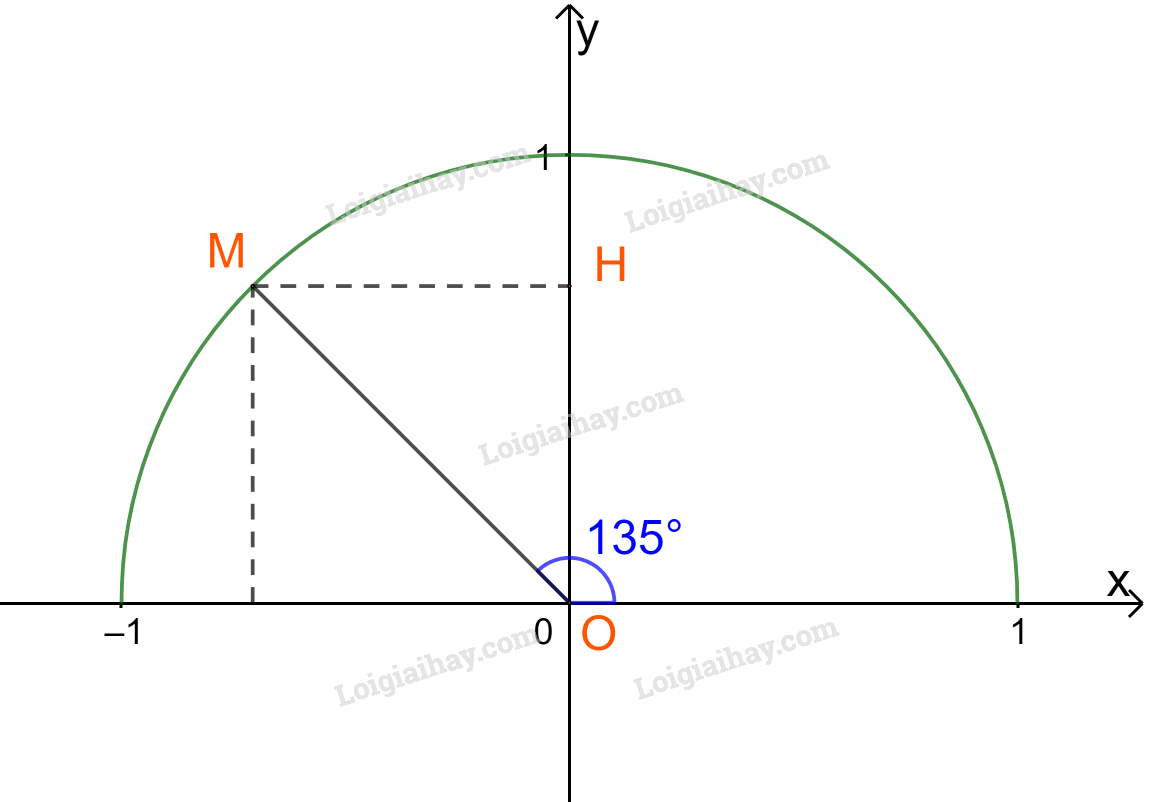
Phương pháp giải:

Tam giác vuông OHM có \(\alpha  = \widehat {xOM}\).

\(\sin \alpha  = \frac{{MH}}{{OM}};\;\cos \alpha  = \frac{{OH}}{{OM}};\;\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}\).

Lời giải chi tiết:

Ta có: tam giác vuông OHM vuông tại H và \(\alpha  = \widehat {xOM}\)

Do đó: \(\sin \alpha  = \frac{{MH}}{{OM}};\;\cos \alpha  = \frac{{OH}}{{OM}}.\)

Mà \(MH = {y_0};OH = {x_0};OM = 1.\)

\( \Rightarrow \sin \alpha  = \frac{{{y_0}}}{1} = {y_0};\;\cos \alpha  = \frac{{{x_0}}}{1} = {x_0}\;.\)

\( \Rightarrow \tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}};\;\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}.\)

Thực hành 1

Tìm các giá trị lượng giác của góc \({135^o}\).

Phương pháp giải:

Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^o}\).

Khi đó hoành độ và tung độ của điểm M lần lượt là các giá trị \(\cos {135^o},\;\sin {135^o}\).

Từ đó suy ra\(\;\tan {135^o} = \frac{{\sin {{135}^o}}}{{\cos {{135}^o}}},\;\;\cot {135^o} = \frac{{\cos {{135}^o}}}{{\sin {{135}^o}}}.\)

Lời giải chi tiết:

Lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^o}\), H là hình chiếu vuông góc của M trên Oy.

Ta có: \(\widehat {MOy} = {135^o} - {90^o} = {45^o}\).

Tam giác OMH vuông cân tại H nên \(OH = MH = \frac{{OM}}{{\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}.\)

Vậy tọa độ điểm M là \(\left( { - \frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right).\)

Vậy theo định nghĩa ta có:

\(\begin{array}{l}\;\sin {135^o} = \frac{{\sqrt 2 }}{2};\;\;\cos {135^o} =  - \frac{{\sqrt 2 }}{2};\\\;\tan {135^o} =  - 1;\;\;\cot {135^o} =  - 1.\end{array}\)

Chú ý

Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc \({135^o}\).

Với loại máy tính fx-570 ES (VN hoặc VN PLUS), ta bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ).

Với loại máy tính fx-580VN X, ta bấm phím “SHIFT” “SETUP” rồi bấm phím “2”, “1” (để chọn đơn vị độ).

Tính \(\sin {135^o}\), bấm phím:  sin  1  3  5  \(^o\)’’’  = ta được kết quả là \(\frac{{\sqrt 2 }}{2}\).

Tính \(\cos {135^o}\),bấm phím:  cos  1  3  5  \(^o\)’’’  = ta được kết quả là \(\frac{{ - \sqrt 2 }}{2}\).

Tính \(\tan {135^o}\), bấm phím:  tan  1  3  5  \(^o\)’’’  = ta được kết quả là \( - 1\).

(Để tính \(\cot {135^o}\), ta tính \(1:\tan {135^o}\)).