Giải mục 2 trang 63 SGK Toán 9 tập 1 - Chân trời sáng tạoa) Tính các tỉ số lượng giác của góc (alpha ) và của góc 90o -(alpha ) trong Hình 8 theo a, b, c. b) So sánh sin (widehat B) và cos (widehat C) , cos (widehat B) và sin (widehat C) , tan (widehat B) và cot (widehat C) , tan (widehat C) và cot (widehat B). Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
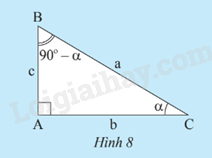
HĐ3 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 3 trang 63 SGK Toán 9 Chân trời sáng tạo a) Tính các tỉ số lượng giác của góc \(\alpha \) và của góc 90o -\(\alpha \) trong Hình 8 theo a, b, c. b) So sánh sin \(\widehat B\) và cos \(\widehat C\) , cos \(\widehat B\) và sin \(\widehat C\) , tan \(\widehat B\) và cot \(\widehat C\) , tan \(\widehat C\) và cot \(\widehat B\).
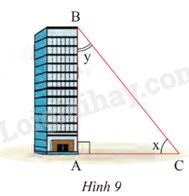
Phương pháp giải: - Dựa vào tỉ số lượng giác của góc nhọn \(\alpha \). Xét tam giác ABC vuông tại A có \(\widehat {ACB} = \alpha \) , ta có: + Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc \(\alpha \) , kí hiệu sin\(\alpha \). + Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc \(\alpha \) , kí hiệu cos\(\alpha \). + Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha \) , kí hiệu tan\(\alpha \). + Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc \(\alpha \) , kí hiệu cot\(\alpha \). Lời giải chi tiết: Xét tam giác ABC vuông tại A. Ta có: Các tỉ số lượng giác của góc \(\alpha \) là: sin \(\alpha \) = \(\frac{{AB}}{{BC}} = \frac{c}{a}\) cos \(\alpha \) = \(\frac{{AC}}{{BC}} = \frac{b}{a}\) tan \(\alpha \) = \(\frac{{AB}}{{AC}} = \frac{c}{b}\) cot \(\alpha \) = \(\frac{1}{{\tan \alpha }} = \frac{b}{c}\) Các tỉ số lượng giác của góc 90o - \(\alpha \) là: sin 90o - \(\alpha \) = \(\frac{{AC}}{{BC}} = \frac{b}{a}\) cos 90o - \(\alpha \) = \(\frac{{AB}}{{BC}} = \frac{c}{a}\) tan 90o - \(\alpha \) = \(\frac{{AC}}{{AB}} = \frac{b}{c}\) cot 90o - \(\alpha \) = \(\frac{1}{{\tan {{90}^o} - \alpha }} = \frac{c}{b}\) b) Ta có \(\widehat C\) = \(\alpha \) ; \(\widehat B\) = 90o - \(\alpha \) nên theo phần a ta có: sin \(\widehat B\) = cos \(\widehat C\) cos \(\widehat B\) = sin \(\widehat C\) tan \(\widehat B\) = cot \(\widehat C\) tan \(\widehat C\) = cot \(\widehat B\) TH3 Video hướng dẫn giải Trả lời câu hỏi Thực hành 3 trang 63 SGK Toán 9 Chân trời sáng tạo a) So sánh: sin 72o và cos 18o ; cos 72o và sin 18o; tan 72o và cot 18o b) Cho biết sin 18o \( \approx 0,31\) ; tan 18o \( \approx 0,32\). Tính cos 72o và cot 72o. Phương pháp giải: - Dựa vào nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia. - Dựa vào VD3 trang 63 làm tương tự. Lời giải chi tiết: a) sin 72o = cos (90 o – 72o)= cos 18o cos 72o = sin(90 o – 72o)= sin 18o tan 72o = cot(90 o – 72o)= cot 18o b) Theo đề bài ta có: sin 18o \( \approx 0,31\) ; tan 18o \( \approx 0,32\). Suy ra cos 72o = sin(90 o – 72o)= sin 18o \( \approx 0,31\) và cot 72o = tan(90 o – 72o)= tan 18o \( \approx 0,32\). VD3 Video hướng dẫn giải Trả lời câu hỏi Vận dụng 3 trang 63 SGK Toán 9 Chân trời sáng tạo Tia nắng chiếu qua điểm B của nóc tòa nhà tạo với mặt đất một góc x và tạo với cạnh AB của tòa nhà một góc y (Hình 9). Cho biết cos x \( \approx 0,78\) và cot x \( \approx 1,25\). Tính sin y và tan y (kết quả làm tròn đến hàng phần trăm).
Phương pháp giải: Dựa vào nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia. Lời giải chi tiết: Xét tam giác ABC vuông tại A, áp dụng tỉ số lượng giác hai góc phụ nhau, ta có: sin y = cos x \( \approx 0,78\) ; tan y = cot x \( \approx 1,25\).
|