Giải mục 2 trang 91, 92, 93 SGK Toán 9 tập 1 - Chân trời sáng tạoVẽ vào vở đường tròn (O) và hai điểm A, B nằm trên (O). Dùng bút chì khác màu tô hai phần của đường tròn được phân chia bởi hai điểm A và B. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
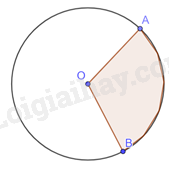
HĐ2 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 2 trang 91 SGK Toán 9 Chân trời sáng tạo Vẽ vào vở đường tròn (O) và hai điểm A, B nằm trên (O). Dùng bút chì khác màu tô hai phần của đường tròn được phân chia bởi hai điểm A và B. Phương pháp giải: Đọc dữ liệu đề bài để vẽ hình. Lời giải chi tiết:
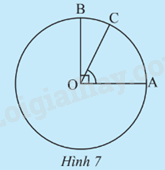
HĐ3 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 3 trang 91 SGK Toán 9 Chân trời sáng tạo Cho OA và OB là hai bán kính vuông góc với nhau của đường tròn (O), C là điểm trên cung nhỏ AB (Hình 7). Ta coi số đo của một cung nhỏ là số đo của góc ở tâm chắn cung đó. a) Xác định số đo cung AB. b) So sánh số đo của hai cung \(\overset\frown{AC}\) và \(\overset\frown{AB}\)
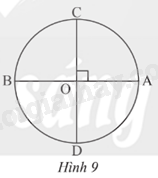
Phương pháp giải: Nhìn hình vẽ xác định số đo \(\overset\frown{AB}=\widehat{AOB}\) và \(\overset\frown{AC}\); \(\overset\frown{AB}\) . Lời giải chi tiết: a) Số đo cung AB bằng \(\widehat {AOB} = {90^o}\). b) Ta có \(\overset\frown{AC}\) < \(\overset\frown{AB}\). TH2 Video hướng dẫn giải Trả lời câu hỏi Thực hành 2 trang 92 SGK Toán 9 Chân trời sáng tạo Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau (Hình 9). Xác định số đo của các cung \(\overset\frown{AB}\),\(\overset\frown{AC}\) và \(\overset\frown{AD}\).
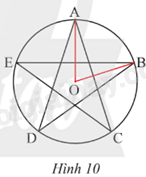
Phương pháp giải: Dựa vào định nghĩa: Số đo cung nhỏ bằng số đo của góc ở tâm chắc cung đó và số đo của cung nửa đường tròn bằng 180o Lời giải chi tiết: Trong Hình 9, ta có cung \(\overset\frown{AB}\) chắn nửa đường tròn nên sđ \(\overset\frown{AB}\) = 180o Cung \(\overset\frown{AC}\) bị chắn bởi góc ở tâm \(\widehat {COA}\) có số đo bằng 90o , suy ra sđ \(\overset\frown{AC}\) = 90o Vì \(AB \bot CD\) tại O nên \(\widehat {AOD} = {90^o}\), cung \(\overset\frown{AD}\) bị chắn bởi góc ở tâm \(\widehat {AOD}\) suy ra sđ \(\overset\frown{AD}\) = 90o. VD2 Video hướng dẫn giải Trả lời câu hỏi Vận dụng 2 trang 92 SGK Toán 9 Chân trời sáng tạo Xác định số đo cung AB trong hình ngôi sao năm cánh (Hình 10).
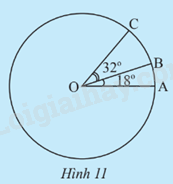
Phương pháp giải: Dựa vào định nghĩa: góc có đỉnh trùng tâm đường tròn là góc ở tâm và tổng góc trong đường tròn bằng 360o Lời giải chi tiết: Ta có hình ngôi sao năm cánh có 5 góc ở tâm bằng nhau vậy mỗi góc là \(\frac{{{{360}^o}}}{5} = {72^o}\) hay sđ \(\overset\frown{AB}\) = 72o. HĐ4 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 4 trang 92 SGK Toán 9 Chân trời sáng tạo Trên đường tròn (O), vẽ hai cung nhỏ \(\overset\frown{AB}\); \(\overset\frown{BC}\) sao cho \(\widehat {AOB} = {18^o};\widehat {BOC} = {32^o}\) và tia OB ở giữa hai tia OA, OC (Hình 11). Tính số đo của các cung \(\overset\frown{AB}\); \(\overset\frown{BC}\); \(\overset\frown{AC}\).
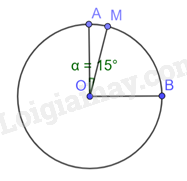
Phương pháp giải: Dựa vào định nghĩa: Số đo cung nhỏ bằng số đo của góc ở tâm chắc cung đó. Lời giải chi tiết: Trong Hình 11, ta có cung \(\overset\frown{AB}\) bị chắn bởi góc ở tâm \(\widehat{AOB}\)có số đo bằng 18o , suy ra sđ \(\overset\frown{AB}\)= 18o Ta có cung \(\overset\frown{BC}\) bị chắn bởi góc ở tâm \(\widehat{BOC}\)có số đo bằng 32o , suy ra sđ \(\overset\frown{BC}\)= 32o Ta có cung \(\overset\frown{AC}\) bị chắn bởi góc ở tâm \(\widehat{AOC}\)có số đo bằng 32o + 18 o = 50 o, suy ra sđ \(\overset\frown{AC}\)= 50o TH3 Video hướng dẫn giải Trả lời câu hỏi Thực hành 3 trang 93 SGK Toán 9 Chân trời sáng tạo Trên cung AB có số đo 90o của đường tròn (O), lấy điểm M sao cho cung AM có số đo 15o. Tính số đo của cung MB. Phương pháp giải: - Đọc dữ kiện đề bài để vẽ hình. - Dựa vào: Trên đường tròn (O), cho M là một điểm nằm trên cung AB. Ta nói điểm M chia cung AB thành hai cung \(\overset\frown{AM}\) và \(\overset\frown{MB}\) suy ra sđ\(\overset\frown{AB}\) = sđ\(\overset\frown{AM}\) + sđ\(\overset\frown{MB}\). Lời giải chi tiết:
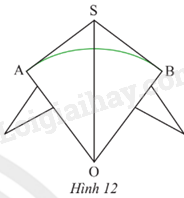
Ta có sđ \(\overset\frown{MB}\) = sđ \(\overset\frown{AB}\) - sđ \(\overset\frown{AM}\) = \({{90}^{o}}-{{15}^{o}}={{75}^{o}}\). VD3 Video hướng dẫn giải Trả lời câu hỏi Vận dụng 3 trang 93 SGK Toán 9 Chân trời sáng tạo Bạn Hùng làm một cái diều với thân diều là hình tứ giác S.AOB sao cho OS là đường phân giác của \(\widehat {AOB}\) và \(\widehat {ASB} = {106^o}\). Thanh tre màu xanh lá được uốn cong thành cung AB của đường tròn tâm O và SA, SB là hai tiếp tuyến của (O) (Hình 12). Tính số đo của \(\overset\frown{AB}\).
Phương pháp giải: - Dựa vào tính chất của tiếp tuyến và tổng các góc của tứ giác bằng 360o - Dựa vào định nghĩa: Số đo cung nhỏ bằng số đo của góc ở tâm chắc cung đó. Lời giải chi tiết: Ta có SA, SB là hai tiếp tuyến của (O) nên OA \( \bot \) SA hay \(\widehat {OAS} = {90^o}\) và OB \( \bot \) SB hay \(\widehat {OBS} = {90^o}\). Xét tứ giác SAOB có \(\widehat {ASB} + \widehat {OAS} + \widehat {AOB} + \widehat {OSB} = {360^o}\) Suy ra \(\widehat {AOB} = {360^o} - \widehat {ASB} - \widehat {OAS} - \widehat {OSB} = {360^o} - {106^o} - {90^o} - {90^o} = {74^o}\) Ta có sđ\(\overset\frown{AB}\) bị chắn bởi góc ở tâm \(\widehat {AOB}\) có số đo bằng 74o suy ra sđ\(\overset\frown{AB}\) = 74o .
|