Giải mục 3 trang 28, 29, 30 SGK Toán 10 tập 1 - Kết nối tri thức

HĐ3

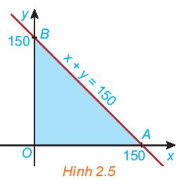
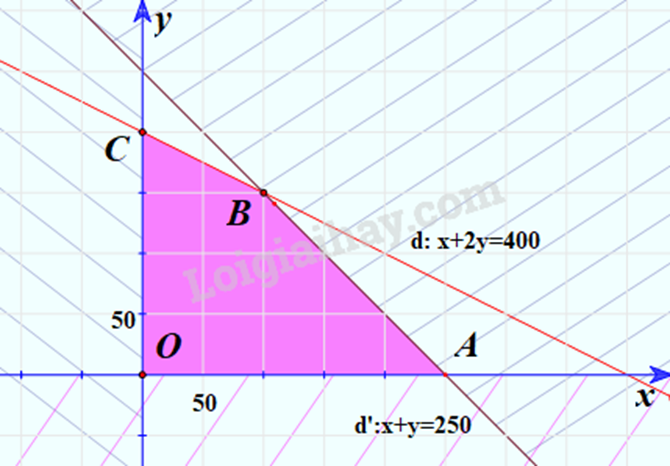
Xét biểu thức F(x, y) = 2x + 3y với (x; y) thuộc miền tam giác OAB ở HĐ2. Toạ độ ba đình là O(0, 0), A(150, 0) và B(0; 150) (H.2.5). 

a) Tính giá trị của biểu thức F(x; y) tại mỗi đỉnh O, A và B.

b) Nêu nhận xét về dấu của hoành độ x và tung độ y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB.

c) Nêu nhận xét về tổng x + y của điểm (X; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị lớn nhất của F(x, y) trên miền tam giác OAB.

Phương pháp giải:

a) Thay tọa độ điểm O, A, B vào F(x;y) và tính giá trị.

b) Lấy một điểm bất kì trong miền tam giác OAB.

Xác định dấu:

+ So sánh x với 0

+ So sánh y với 0

Đánh giá biểu thức F(x;y) dựa vào dấu của x và y, từ đó tìm giá trị nhỏ nhất của biểu thức.

c)

Dựa vào biểu thức

Giá trị lớn nhất: Tách 2x+3y =2.(x+y)+y và dựa vào việc đánh giá x+y và y ở bước trên để tìm giá trị lớn nhất.

Lời giải chi tiết:

a) Thay tọa độ điểm O, A, B vào F(x;y) ta được:

F(0;0)=2.0+3.0=0

F(150;0)=2.150+3.0=300

F(0;150)=2.0+3.150=450.

b) Lấy một điểm bất kì trong miền tam giác OAB.

Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(x \ge 0\).

Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(y \ge 0\).

Vậy \(x \ge 0\) và \(y \ge 0\).

=> \(F\left( {x;y} \right) = 2x + 3y \ge 2.0 + 3.0 = 0\)

Vậy giá trị nhỏ nhất của F(x;y) trên miền OAB là 0.

c) Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(x + y \le 150\)

Như vậy với mỗi điểm trong miền tam giác OAB thì đều có tổng \(x + y \le 150\)

Quan sát miền OAB ta thấy điểm B(0;150) là điểm có tung độ lớn nhất nên mọi điểm (x;y) thuộc miền OAB đều có \(y \le 150\).

Vậy ta có: \(F\left( {x;y} \right) = 2x + 3y\)\( = 2.\left( {x + y} \right) + y\)\( \le 2.150 + 150 = 450\)

Dấu “=” xảy ra khi x+y=150 và y=150. Hay x=0, y=150.

Giá trị lớn nhất trên miền OAB là 450 tại điểm B.

Vận dụng

Một cửa hàng có kế hoạch nhập về hai loại máy tính A và B, giá mỗi chiếc lần lượt là 10 triệu đồng và 20 triệu đồng với số vốn ban đầu không vượt quá 4 tỉ đồng. Loại máy A mang lại lợi nhuận 2,5 triệu đồng cho mỗi máy bán được và loại máy B mang lại lợi nhuận là 4 triệu đồng mỗi máy. Cửa hàng ước tính rằng tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy. Giả sử trong một tháng cửa hàng cần nhập số máy tính loại A là x và số máy tính loại B là y.

a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương

trình rồi xác định miền nghiệm của hệ đó.

b) Gọi F (triệu đồng) là lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B. Hãy biểu diễn F theo x và y.

c) Tìm số lượng máy tính mỗi loại cửa hàng cần nhập về trong tháng đó đề lợi nhuận thu được là lớn nhất.

Phương pháp giải:

a)

Bước 1: Lập bảng thể hiện vốn và lợi nhuận của mỗi loại máy.

Bước 2: Dựa vào các điều kiện sau để lập bất phương trình:

+ Số lượng là số tự nhiên

+ Điều kiện vốn ban đầu

+ Nhu cầu hàng tháng

Bước 3: Xác định miền nghiệm.

b) Lợi nhuận hàng tháng bằng lợi nhuận bán x máy loại A và y máy loại B.

c)

Bước 1: Xác định giá trị của F tại các điểm thuộc miền đa giác biểu diễn miền nghiệm của hệ bất phương trình ở câu a.

Bước 2: Giá trị lớn nhất của F là số lớn nhất trong các số tìm được ở bước 1.

Lời giải chi tiết:

a) Số máy tính loại A cửa hàng cần nhập trong một tháng là \(x\) (máy), số máy tính loại B cửa hàng cần nhập trong một tháng là \(y\) (máy).

Do tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy nên \(x + y \le 250\).

Vì mỗi chiếc máy tính loại A có giá 10 triệu và mỗi máy tính loại B có giá 20 triệu nên tổng số vốn cửa hàng cần nhập hai loại A và B là \(10x + 20y\) (triệu đồng).

Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên \(10x + 20y \le 4000\) hay \(x + 2y \le 400\).

Ta có hệ bất phương trình: \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 250\\x + 2y \le 400\end{array} \right.\).

Ta xác định miền nghiệm của hệ bất phương trình trên:

- Miền nghiệm \(D_1\) của bất phương trình \(x \ge 0\) là nửa mặt phẳng bờ \(Oy\) chứa điểm \((1;0)\).

- Miền nghiệm \(D_2\) của bất phương trình \(y \ge 0\) là nửa mặt phẳng bờ \(Ox\) chứa điểm \((0;1)\).

- Xác định miền nghiệm \(D_3\) của bất phương trình \(x + y \le 250\).

+ Vẽ đường thẳng \(d: x + y = 250\).

+ Vì \(0 + 0 = 0 < 250\) nên tọa độ điểm \(O(0;0)\) thỏa mãn bất phương trình \(x + y \le 250\).

Do đó miền nghiệm \(D_3\)  của bất phương trình \(x + y \le 250\) là nửa mặt phẳng bờ \(d\) chứa gốc tọa độ.

- Xác định miền nghiệm \(D_4\) của bất phương trình \(x + 2y \le 400\).

+ Vẽ đường thẳng \(d’: x + 2y  = 400\).

+ Vì \(0 + 2.0 = 0 < 400\) nên tọa độ điểm \(O(0;0)\) thỏa mãn bất phương trình \(x + 2y < 400\).

Do đó miền nghiệm \(D_4\) của bất phương trình \(x + 2y < 400\) là nửa mặt phẳng bờ \(d’\) chứa gốc tọa độ.

Miền nghiệm của hệ bất phương trình trên là tứ giác OABC với \(O(0;0)\), \(A(0; 200)\), \(C(100;150)\), \(B(250;0)\).

b) Lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B là: \(F(x;y) = 2,5x + 4y\) (triệu đồng).

c) Bài toán trở thành tìm giá trị lớn nhất của \(F(x;y)\) với \((x;y)\) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 250\\x + 2y \le 400\end{array} \right.\).

Người ta đã chứng minh được, giá trị \(F(x; y)\) lớn nhất tại \((x; y)\) là tọa độ của một trong bốn đỉnh \(O\), \(A\), \(B\), \(C\).

Tại \(O(0; 0)\), ta có: \(F(0; 0) = 2,5 . 0 + 4 . 0 = 0\);

Tại \(A(0; 200)\), ta có: \(F(0; 200) = 2,5 . 0 + 4 . 200 = 800\);

Tại \(B(100; 150)\), ta có: \(F(100; 150) = 2,5 . 100 + 4 . 150 = 850\);

Tại \(B(250; 0)\), ta có: \(F(250; 0) = 2,5 . 250 + 4 . 0 = 625\).

Do đó \(F(x;y)\) lớn nhất bằng \(850\) tại \(x = 100\) và \(y = 150\).

Vậy cửa hàng cần đầu tư kinh doanh 100 máy A và 150 máy B.