Lý thuyết Các phép toán trên tập hợp - SGK Toán 10 Chân trời sáng tạo1. Hợp và giao của các tập hợp 2. Hiệu của hai tập hợp, phần bù của tập con Quảng cáo
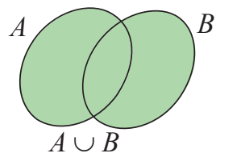
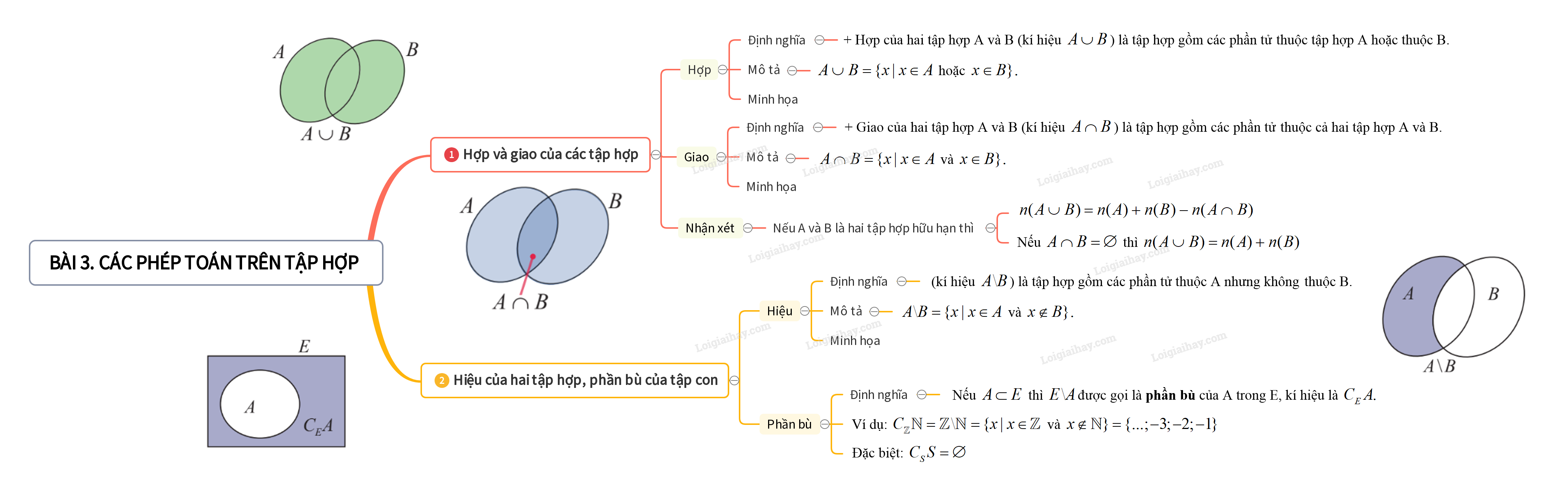
1. Hợp và giao của các tập hợp + Hợp của hai tập hợp A và B (kí hiệu \(A \cup B\)) là tập hợp gồm các phần tử thuộc tập hợp A hoặc thuộc T. \(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} .\) + Giao của hai tập hợp A và B (kí hiệu \(A \cap B\)) là tập hợp gồm các phần tử thuộc cả hai tập hợp A và B. \(A \cap B = \{ x|x \in A\) và \(x \in B\} .\) + Nhận xét: Nếu A và B là hai tập hợp hữu hạn thì \(n(A \cup B) = n(A) + n(B) - n(A \cap B)\) Nếu \(A \cap B = \emptyset \) thì \(n(A \cup B) = n(A) + n(B)\)
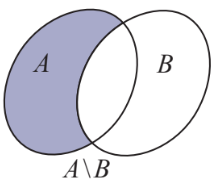
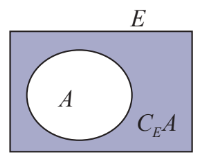
2. Hiệu của hai tập hợp, phần bù của tập con Hiệu của hai tập hợp A và B (kí hiệu \(A{\rm{\backslash }}B\)) là tập hợp gồm các phần tử thuộc A nhưng không thuộc B. \(A{\rm{\backslash }}B = \{ x|x \in A\) và \(x \notin B\} .\) Nếu \(A \subset E\) thì \(E{\rm{\backslash }}A\)được gọi là phần bù của A trong E, kí hiệu là \({C_E}A.\) Ví dụ: \({C_\mathbb{Z}}\mathbb{N} = \mathbb{Z}{\rm{\backslash }}\mathbb{N} = \{ x|x \in \mathbb{Z}\) và \(x \notin \mathbb{N}\} = \{ ...; - 3; - 2; - 1\} \) Đặc biệt: \({C_S}S = \emptyset \)
|