Ý nghĩa hình học, vật lí của đạo hàm - Toán 11

Tiếp tuyến của đồ thị hàm số y = f(x) tại điểm \(P\left( {{x_0};f({x_0})} \right)\) là đường thẳng đi qua P với hệ số góc \(k = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}\) nếu giới hạn này tồn tại và hữu hạn, nghĩa là \(k = f'({x_0})\). Điểm P gọi là tiếp điểm.

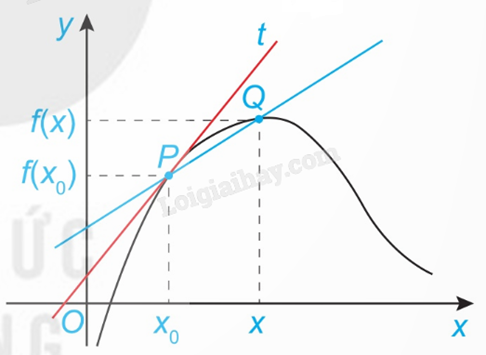
Nếu hàm số y = f(x) có đạo hàm tại điểm \({x_0}\) thì phương trình tiếp tuyến của đồ thị hàm số tại điểm \(P\left( {{x_0};{y_0}} \right)\) là \(y - {y_0} = f'({x_0})(x - {x_0})\), trong đó \({y_0} = f({x_0})\).

a) Vận tốc tức thời

Xét chuyển động thẳng xác định bởi phương trình \(s = s(t)\), với \(s = s(t)\) là một hàm số có đạo hàm. Như đã thấy trong bài toán mở đầu, vận tốc tức thời của chuyển động tại thời điểm \({t_0}\) là đạo hàm của hàm số \(s = s(t)\) tại \({t_0}\):

\(v({t_0}) = s'({t_0})\).

b) Cường độ tức thời

Nếu điện lượng \(Q\) truyền trong dây dẫn là một hàm số của thời gian: \(Q = Q(t)\) (\(Q = Q(t)\) là một hàm số có đạo hàm) thì cường độ tức thời của dòng điện tại thời điểm \({t_0}\) là đạo hàm của hàm số \(Q = Q(t)\) tại \({t_0}\):

\(I({t_0}) = Q'({t_0})\).