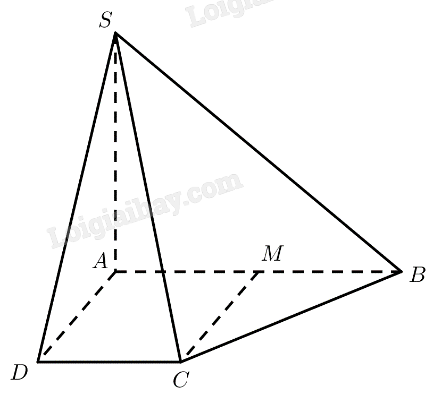
Bài 1 trang 64 SGK Toán 11 tập 2 – Chân trời sáng tạoCho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\). Cho biết \(ABCD\) là hình thang vuông tại \(A\) và \(D\), \(AB = 2CD\). a) Chứng minh \(CD \bot \left( {SAD} \right)\). b) Gọi \(M\) là trung điểm của \(AB\). Chứng minh \(CM \bot \left( {SAB} \right)\). Quảng cáo
Đề bài Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\). Cho biết \(ABCD\) là hình thang vuông tại \(A\) và \(D\), \(AB = 2CD\). a) Chứng minh \(CD \bot \left( {SAD} \right)\). b) Gọi \(M\) là trung điểm của \(AB\). Chứng minh \(CM \bot \left( {SAB} \right)\). Phương pháp giải - Xem chi tiết Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng. Lời giải chi tiết a) Ta có: \(\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot CD\\AB \bot CD\end{array} \right\} \Rightarrow CD \bot \left( {SAD} \right)\). b) Ta có: \(\left. \begin{array}{l}AB\parallel CD \Rightarrow AM\parallel CD\\AM = CD\left( { = \frac{1}{2}AB} \right)\end{array} \right\}\) \( \Rightarrow AMCD\) là hình bình hành. Lại có: \(\widehat {MAD} = {90^ \circ }\). Vậy \(AMCD\) là hình chữ nhật. \(\left. \begin{array}{l} \Rightarrow CM \bot AB\\SA \bot \left( {ABCD} \right) \Rightarrow SA \bot CM\end{array} \right\} \Rightarrow CM \bot \left( {SAB} \right)\).  Chia sẻ Bình luận
Group 2K9 Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
