Bài 5 trang 33 SGK Toán 11 tập 1 - Chân trời sáng tạo

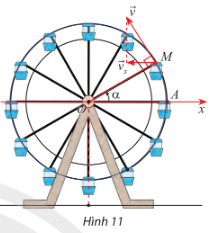
Đề bài

Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin M phụ thuộc vào góc lượng giác \(\alpha \; = \;(Ox,OM)\) theo hàm số \({v_x} = 0,3sin\alpha \;\) (m/s) (Hình 11).

a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của \({v_x}\)

b) Dựa vào đồ thị của hàm số sin, hãy cho biết trong vòng quay đầu tiên \((0 \le \alpha  \le 2\alpha )\), góc \(\alpha \) ở trong các khoảng nào thì \({v_x}\) tăng.

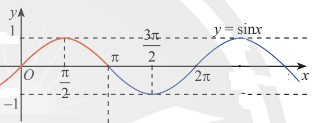
Lời giải chi tiết

a) Do \( - 1 \le sin\alpha  \le 1\;\)nên \( - 0,3 \le sin\alpha  \le 0,3\)

Vậy giá trị lớn nhất của \({v_x}\) là 0,3 (m) và giá trị nhỏ nhất của \({v_x}\) là -0,3 (m).

b) Ta có đồ thị hàm số:

 

Với góc \(\alpha  \in \left( {0;\frac{\pi }{2}} \right)\) hoặc \(\alpha  \in \left( {\frac{{3\pi }}{2};2\pi } \right)\) thì \({v_x}\) tăng.