Bài 7 trang 120 SGK Toán 11 tập 1 - Cánh Diều

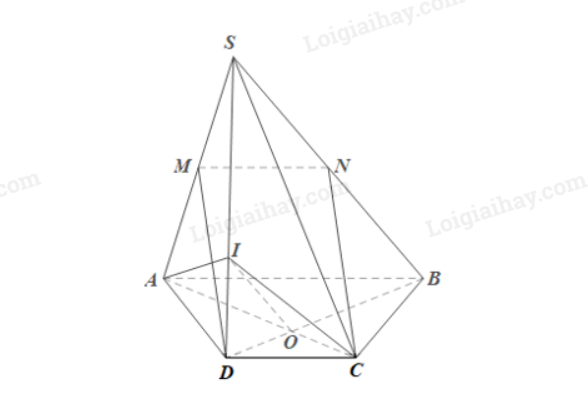
Đề bài

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD) và AB = 2CD. Gọi M, N lần lượt là trung điểm của các cạnh SA, SB.

a) Chứng minh rằng MN // (SCD).

b) Chứng minh rằng DM // (SBC).

c) Lấy điểm I thuộc cạnh SD sao cho \(\frac{{SI}}{{SD}} = \frac{2}{3}\). Chứng minh rằng: SB // (AIC).

Lời giải chi tiết

a) Trong mặt phẳng (SAB), xét ΔSAB có M, N lần lượt là trung điểm của SA, SB nên MN là đường trung bình của ΔSAB.

Do đó MN // AB.

Mà AB // CD (giả thiết) nên MN // CD.

Lại có CD ⊂ (SCD) nên MN // (SCD).

b) Theo câu a, MN là đường trung bình của ΔSAB nên MN = ½ AB.

Mà AB = 2CD hay CD = ½ AB.

Do đó MN = CD.

Xét tứ giác MNCD có: MN // CD và MN = CD nên MNCD là hình bình hành.

Suy ra DM // CN.

Mà CN ⊂ (SBC) nên DM // (SBC).

c) Trong mặt phẳng (ABCD), gọi O là giao điểm của AC và BD.

Do AB // CD, theo hệ quả định lí Thalès ta có: \(\frac{{OB}}{{DO}} = \frac{{AB}}{{CD}} = \frac{2}{1}\).

Suy ra \(\frac{{OB}}{{DO + OB}} = \frac{2}{{1 + 2}} = \frac{2}{3}\) hay \(\frac{{OB}}{{DO}} = \frac{2}{3}\).

Trong mặt phẳng (SDB), xét ΔSDB có \(\frac{{SI}}{{SD}} = \frac{{OB}}{{DB}} = \frac{2}{3}\) nên IO // SB (theo định lí Thalès đảo).

Mà IO ⊂ (AIC) nên SB // (AIC).