Bài 8 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạoCho hình lăng trụ (ABC.A'B'C'). Gọi (M,N,P,Q) lần lượt là trung điểm của các cạnh (AC,AA',A'C',BC). Ta có: GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn Quảng cáo
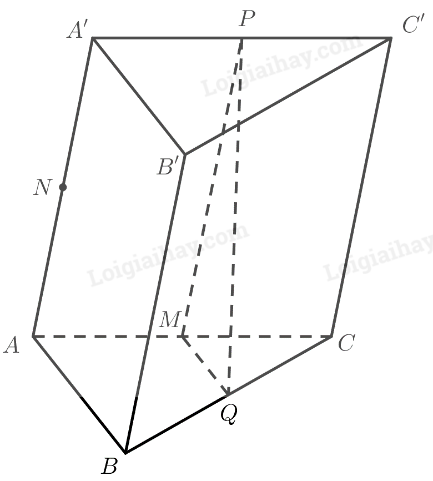
Đề bài Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(M,N,P,Q\) lần lượt là trung điểm của các cạnh \(AC,AA',A'C',BC\). Ta có: A. \(\left( {MNP} \right)\parallel \left( {BCA} \right)\). B. \(\left( {MNQ} \right)\parallel \left( {A'B'C'} \right)\). C. \(\left( {NQP} \right)\parallel \left( {CAB} \right)\). D. \(\left( {MPQ} \right)\parallel \left( {ABA'} \right)\). Phương pháp giải - Xem chi tiết Sử dụng định lí: Nếu mặt phẳng \(\left( P \right)\) chứa hai đường thẳng \(a,b\) cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng \(\left( Q \right)\) thì \(\left( P \right)\) song song với \(\left( Q \right)\). Lời giải chi tiết
Ta có: \(M\) là trung điểm của \(AC\) \(Q\) là trung điểm của \(BC\) \( \Rightarrow MQ\) là đường trung bình của tam giác \(ABC\) \(\left. \begin{array}{l} \Rightarrow MQ\parallel AB\\AB \subset \left( {ABA'} \right)\end{array} \right\} \Rightarrow MQ\parallel \left( {ABA'} \right)\) \(M\) là trung điểm của \(AC\) \(P\) là trung điểm của \(A'C'\) \( \Rightarrow MP\) là đường trung bình của hình bình hành \(ACC'A'\) \(\left. \begin{array}{l} \Rightarrow MP\parallel AA'\\AA' \subset \left( {ABA'} \right)\end{array} \right\} \Rightarrow MP\parallel \left( {ABA'} \right)\) \(\left. \begin{array}{l}MQ\parallel \left( {ABA'} \right)\\MP\parallel \left( {ABA'} \right)\\MP,MQ \subset \left( {MPQ} \right)\end{array} \right\} \Rightarrow \left( {MPQ} \right)\parallel \left( {ABA'} \right)\) Chọn D.  Chia sẻ Bình luận
Tham Gia Group Dành Cho Lớp 11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
