Bài 1.83 trang 41 SBT giải tích 12Giải bài 1.83 trang 41 sách bài tập giải tích 12. Chứng minh rằng phương trình... GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn Quảng cáo
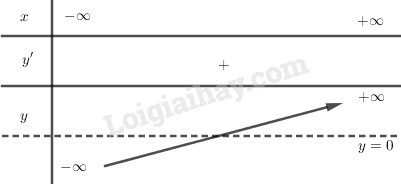
Đề bài Chứng minh rằng phương trình \(3{x^5} + 15x-8 = 0\) chỉ có một nghiệm thực. Phương pháp giải - Xem chi tiết - Xét tính đơn điệu của hàm số trên TXĐ. - Chứng tỏ phương trình có nghiệm, từ đó suy ra điều phải chứng minh. Lời giải chi tiết Hàm số \(f(x) = 3{x^5} + 15x - 8\) là hàm số liên tục và có đạo hàm trên \(\mathbb{R}\). Có \(y' = 15{x^4} + 5 > 0,\forall x \in \mathbb{R}\) nên hàm số đã cho luôn luôn đồng biến. Mà \(f(0) = - 8 < 0,f(1) = 10 > 0\)\( \Rightarrow f\left( 0 \right).f\left( 1 \right) < 0\) nên tồn tại ít nhất một số \({x_0} \in (0;1)\) sao cho \(f\left( {{x_0}} \right) = 0\), tức là phương trình \(f\left( x \right) = 0\) có nghiệm. Mà hàm số đồng biến trên R nên điểm này là duy nhất. Vậy phương trình chỉ có một nghiệm duy nhất (đpcm). Cách khác: Hàm số \(f(x) = 3{x^5} + 15x - 8\) là hàm số liên tục và có đạo hàm trên \(\mathbb{R}\). Có \(y' = 15{x^4} + 5 > 0,\forall x \in \mathbb{R}\) nên hàm số đã cho luôn luôn đồng biến trên \(\mathbb{R}\). Ta có: \(\begin{array}{l} Bảng biến thiên:
Từ bbt ta thấy đường thẳng y=0 luôn cắt đồ thị hàm số y=f(x) tại duy nhất 1 điểm hay pt đã cho có nghiệm duy nhất. Loigiaihay.com
|