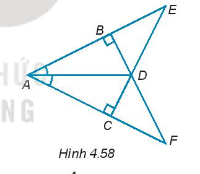
Giải bài 4.56 trang 73 sách bài tập toán 7 - Kết nối tri thức với cuộc sống

Đề bài

Cho các điểm A, B, C, D, E, F như Hình 4.58.

a) Tìm ba cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.

b) Chứng minh \(\Delta ADE = \Delta ADF\).

Lời giải chi tiết

a)

- Xét \(\Delta ABD\) và \(\Delta ACD\) có:

AD: Cạnh chung

\(\widehat {DAB} = \widehat {DAC} (gt)\)

\(\widehat {ABD} = \widehat {ACD} = {90^0}\)

Vậy \(\Delta ABD = \Delta ACD\left( {ch - gn} \right)\)

- Xét \(\Delta ABF\) và \(\Delta ACE\) có:

\(\begin{array}{l}AB = AC\left( \text{do } \Delta ABD = \Delta ACD \right)\\\widehat A: \text{ chung}\\\widehat {ABF} = \widehat {ACE} = {90^0}\end{array}\)

Vậy \(\Delta ABF = \Delta ACE\left( {ch - cgv} \right)\)

- Xét \(\Delta BDE\) và \(\Delta CDF\) có:

\(\begin{array}{l}\widehat {DBE} = \widehat {DCF} = {90^0}\\BD = CD\left(\text{do } \Delta ABD = \Delta ACD \right)\\\widehat {BDE} = \widehat {CDF}\left( \text{hai góc đối đỉnh} \right)\end{array}\)

Vậy \(\Delta BDE = \Delta CDF\left( {g - c - g} \right)\)

b) Ta có:

\(\Delta ABF = \Delta ACE\left( {cmt} \right) \) nên \(AF = AE\)

\(\Delta BDE = \Delta CDF\left( {cmt} \right) \) nên \(\widehat E = \widehat F\)

Xét \(\Delta ADE\) và \(\Delta ADF\) có:

\(AD\): Cạnh chung

\(AE = AF (cmt)\)

\(\begin{array}{l}\widehat E = \widehat F\left( {cmt} \right) \end{array}\) 

Vậy \(\Delta ADE = \Delta ADF\left( {c - g - c} \right)\)