Giải bài 7.48 trang 42 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Đề bài

Cho lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Khoảng cách từ điểm A đến đường thẳng BB’ bằng.

A. \(\frac{{a\sqrt 7 }}{2}\).

B. \(\frac{{a\sqrt {14} }}{4}\).

C. \(\frac{{a\sqrt 7 }}{4}\).

D. \(\frac{{a\sqrt {14} }}{2}\),

Lời giải chi tiết

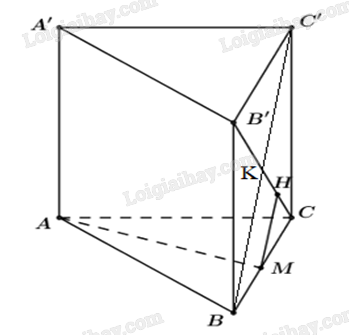
Gọi \(M\) là trung điểm \(BC\)

\(B'C \cap BC' = K\)

\(H\) là trung điểm \(KC\)

Do tứ giác \(BCC'B'\) là hình vuông suy ra \(B'C \bot BC';HM \bot B'C\,\,(1)\)

Dễ thấy \(AM \bot \left( {BCC'B'} \right) \Rightarrow AM \bot B'C{\kern 1pt} {\kern 1pt} \,\,\,(2)\)

Từ \(\left( 1 \right);\left( 2 \right) \Rightarrow \left( {AMH} \right) \bot B'C \Rightarrow AH \bot B'C\)

Từ đó suy ra khoảng cách từ điểm  đến đường thẳng \(B'C\) bằng \(AH\)

Ta có \(AM = \frac{{a\sqrt 3 }}{2};HM = \frac{{BK}}{2} = \frac{{{\rm{a}}\sqrt 2 }}{4}\)

Xét tam giác \(AMH\) vuông tại \(M\) ta có \(AH = \sqrt {A{M^2} + H{M^2}}  = \frac{{a\sqrt {14} }}{4}\)

Vậy, khoảng cách từ điểm  đến đường thẳng \(B'C\) bằng \(\frac{{a\sqrt {14} }}{4}\)