Giải bài 8 trang 120 SGK Toán 7 tập 2 - Cánh diềuCho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc với OA, OB, OC, hai trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 144). Chứng minh: GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn Quảng cáo
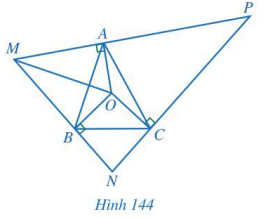
Đề bài Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc với OA, OB, OC, hai trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 144). Chứng minh: a) \(\Delta OMA = \Delta OMB\) và tia MO là tia phân giác của góc NMP; b) O là giao điểm của ba đường phân giác của tam giác MNP.
Phương pháp giải - Xem chi tiết a) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông. b) Chứng minh dựa vào kết quả của phần a). Lời giải chi tiết a) O là giao điểm của ba đường trung trực của tam giác ABC nên O cách đều ba đỉnh của tam giác đó hay OA = OB = OC. Xét hai tam giác vuông OAM và OBM có: OA = OB; OM chung. Vậy \(\Delta OAM = \Delta OBM\)(cạnh huyền – cạnh góc vuông). Suy ra: \(\widehat {OMA} = \widehat {BMO}\) ( 2 góc tương ứng). Vậy MO là tia phân giác của góc BMA hay MO là tia phân giác của góc NMP (ba điểm M, A, P thẳng hàng và ba điểm M, B, N thẳng hàng). b) MO là tia phân giác của góc NMP. Tương tự ta có: NO là tia phân giác của góc MNP. PO là tia phân giác của góc MPN. Vậy O là giao điểm của ba đường phân giác MO, NO, PO của tam giác MNP.  Chia sẻ Bình luận
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
