Giải câu hỏi mở đầu trang 57 SGK Toán 11 tập 1 - Chân trời sáng tạo

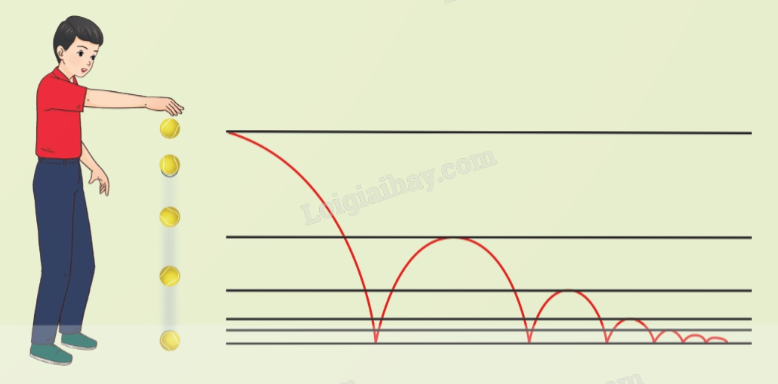
Đề bài

Một quả bóng rơi từ một vị trí có độ cao 120 cm. Khi chạm đất, nó luôn nảy lên độ cao bằng một nửa độ cao của lần rơi trước đó.

Gọi \({u_1} = 120\) là độ cao của lần rơi đầu tiên và \({u_2};{u_3};...;{u_n};...\) là độ cao của các lần rơi kế tiếp. Tìm 5 số hạng đầu tiên của dãy \(({u_n})\) và tìm điểm đặc biệt của dãy số đó.

Lời giải chi tiết

Ta có: \({u_1} = 120\).

Vì độ cao sau bằng một nửa độ cao của lần rơi trước đó nên ta có:

\({u_2} = \frac{1}{2}{u_1} = \frac{1}{2} \cdot 120 = 60\);

\({u_3} = \frac{1}{2}{u_2} = \frac{1}{2} \cdot 60 = 30\);

\({u_4} = \frac{1}{2}{u_3} = \frac{1}{2} \cdot 30 = 15\);

\({u_5} = \frac{1}{2}{u_4} = \frac{1}{2} \cdot 15 = 7,5.\)

Điểm đặc biệt của dãy số là:

Dãy số giảm dần và mỗi số hạng sau đều bằng tích của số hạng ngay trước nó với một số \(q\) không đổi là \(q = \frac{1}{2}\).