Giải mục 3 trang 26, 27 SGK Toán 11 tập 1 - Cánh Diều

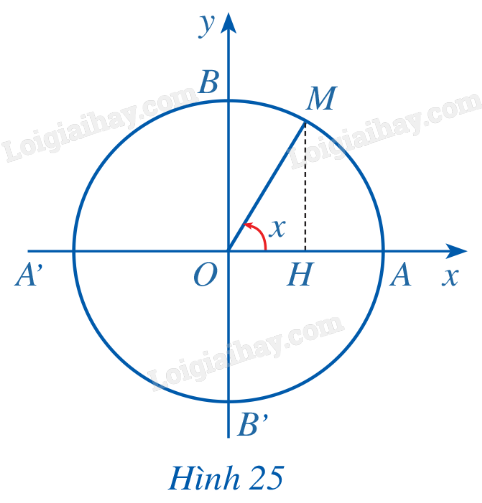
HĐ6

Trả lời câu hỏi Hoạt động 6 trang 26 SGK Toán 11 Cánh diều

Với mỗi số thực x, tồn tại duy nhất điểm M trên đường tròn lượng giác sao cho \(\left( {OA,OM} \right) = x\left( {rad} \right)\) (Hình 25). Hãy xác định \(\cos x\).

Phương pháp giải:

Sử dụng công thức tính giá trị của cosin.

Lời giải chi tiết:

\(\cos x = \frac{{OH}}{{OM}}\).

HĐ7

Trả lời câu hỏi Hoạt động 7 trang 26 SGK Toán 11 Cánh diều

Cho hàm số \(y = \cos x\).

a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

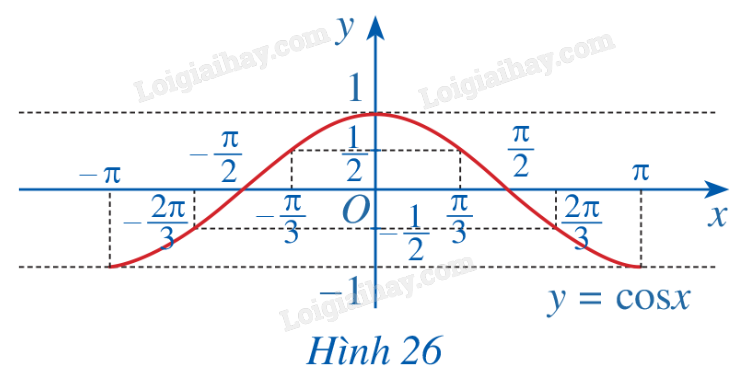
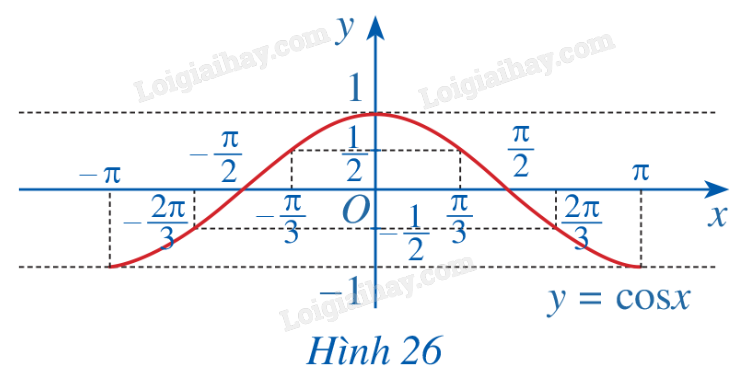
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 26).

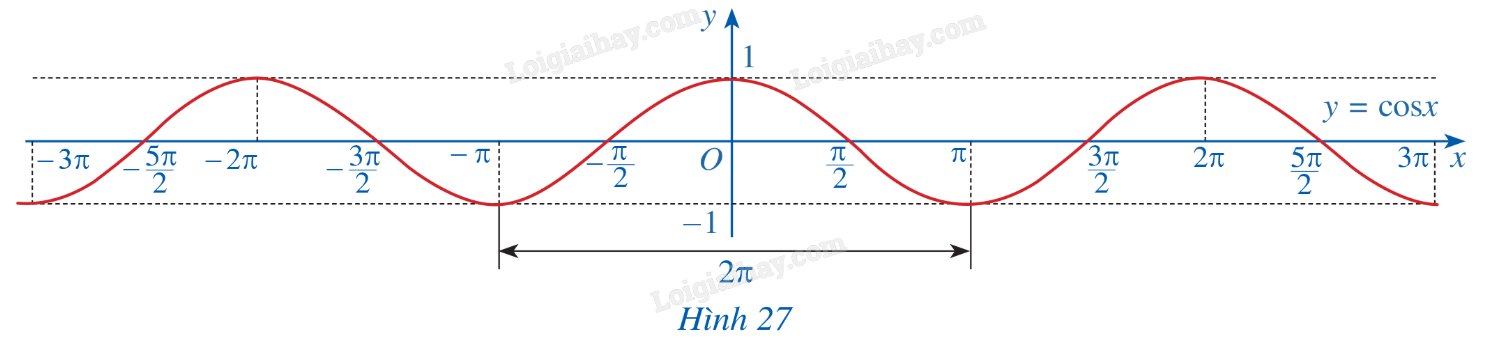
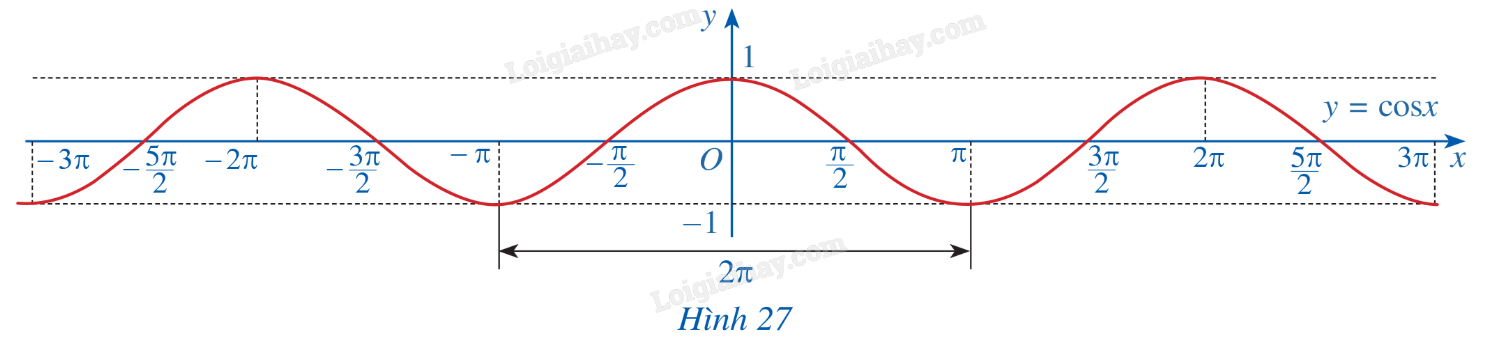
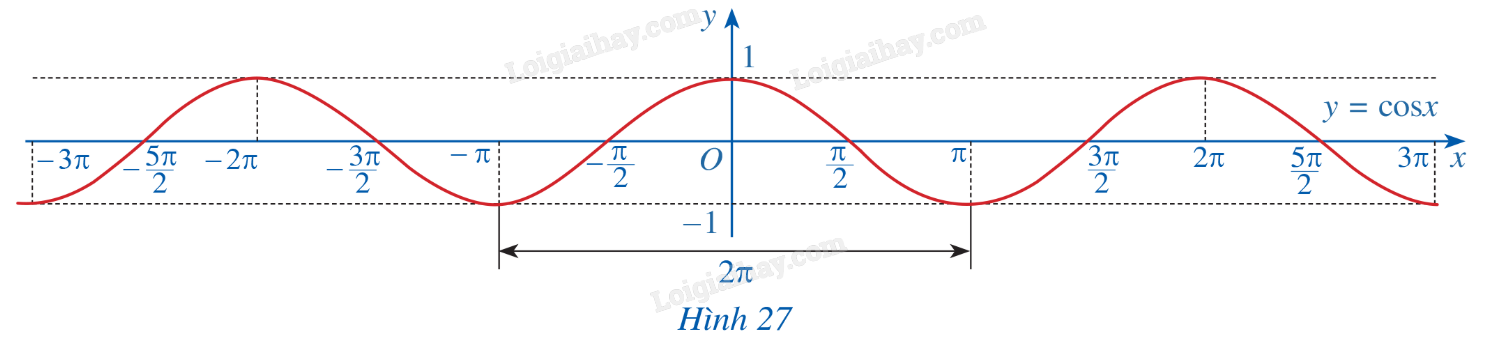
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\) trên R được biểu diễn ở Hình 27.

Phương pháp giải:

Sử dụng công thức tính giá trị của cosin.

Lời giải chi tiết:

a)

b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 26).

c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.

HĐ8

Trả lời câu hỏi Hoạt động 8 trang 27 SGK Toán 11 Cánh diều

Quan sát đồ thị \(y = \cos x\) ở Hình 27.

a) Nêu tập giá trị của hàm số \(y = \cos x\).

b) Trục tung có là trục đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số \(y = \cos x\).

c) Bằng cách dịch chuyển đồ thị \(y = \cos x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị có hàm số \(y = \cos x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\) hay không? Hàm số \(y = \cos x\) có tuần hoàn hay không?

d) Tìm khoảng đồng biến, nghịch biến của hàm số \(y = \cos x\).

Phương pháp giải:

Sử dụng định nghĩa về hàm số cosin.

Lời giải chi tiết:

a) Tập giá trị của hàm số \(y = \cos x\)là \(\left[ { - 1;1} \right]\).

b) Trục tung là trục đối xứng của hàm số \(y = \cos x\).

Như vậy hàm số \(y = \cos x\) là hàm số chẵn.

c) Bằng cách dịch chuyển đồ thị \(y = \cos x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị có hàm số \(y = \cos x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\).

Như vậy hàm số \(y = \cos x\) là hàm số tuần hoàn.

d) Hàm số \(y = \cos x\) đồng biến trên mỗi khoảng \(\left( { - \pi  + k2\pi ;k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi  + k2\pi } \right)\) với \(k \in Z\).

LT-VD4

Trả lời câu hỏi Luyện tập - Vận dụng 4 trang 27 SGK Toán 11 Cánh diều

Hàm số \(y = \cos x\) đồng biến hay nghịch biến trên khoảng \(\left( { - 2\pi ; - \pi } \right)\).

Phương pháp giải:

Sử dụng khoảng đồng biến, nghịch biến của hàm số cosin:

Hàm số \(y = \cos x\) đồng biến trên mỗi khoảng \(\left( { - \pi  + k2\pi ;k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi  + k2\pi } \right)\) với \(k \in Z\).

Lời giải chi tiết:

Do \(\left( { - 2\pi ; - \pi } \right) = \left( { - 2\pi ;\pi  - 2\pi } \right)\) nên hàm số \(y = \cos x\) nghịch biến trên khoảng \(\left( { - 2\pi ; - \pi } \right)\).