Giải mục 4 trang 22, 23 SGK Toán 11 tập 1 - Chân trời sáng tạoÁp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác (alpha = frac{{alpha + beta }}{2},beta = frac{{alpha - beta }}{2}) ta được đẳng thức nào? Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
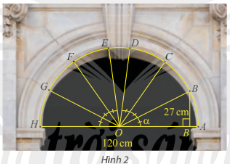
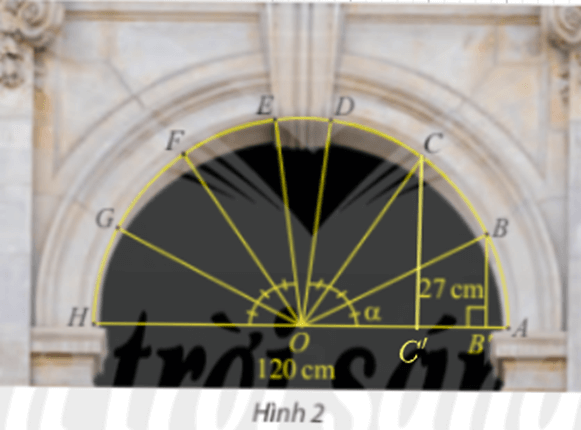
HĐ4 Trả lời câu hỏi Hoạt động 4 trang 22 SGK Toán 11 Chân trời sáng tạo Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác \(a = \frac{{\alpha + \beta }}{2}\), \(b = \frac{{\alpha - \beta }}{2}\) ta được đẳng thức nào? Phương pháp giải: Áp dụng công thức: \(\begin{array}{l}\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right]\\\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a - b} \right) - \cos \left( {a + b} \right)} \right]\\\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right]\end{array}\) Lời giải chi tiết: Ta có: \(\begin{array}{l}\cos a\cos b = \cos \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos a + \cos b } \right)\end{array}\) \(\begin{array}{l}\sin a \sin b = \sin \frac{{\alpha + \beta }}{2}\sin \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right) - \cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos b - \cos a } \right)\end{array}\) \(\begin{array}{l}\sin a \cos b = \sin \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\sin \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \sin \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\sin a + \sin b } \right)\end{array}\) TH4 Trả lời câu hỏi Thực hành 4 trang 23 SGK Toán 11 Chân trời sáng tạo Tính \(\cos \frac{{7\pi }}{{12}} + \cos \frac{\pi }{{12}}\). Phương pháp giải: Áp dụng công thức: \(\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\). Lời giải chi tiết: Ta có: \(\begin{array}{l}\cos \frac{{7\pi }}{{12}} + \cos \frac{\pi }{{12}} = 2\cos \frac{{\frac{{7\pi }}{{12}} + \frac{\pi }{{12}}}}{2}\cos \frac{{\frac{{7\pi }}{{12}} - \frac{\pi }{{12}}}}{2}\\ = 2.\frac{1}{2}.\frac{{\sqrt 2 }}{2} = \frac{{\sqrt 2 }}{2}.\end{array}\) VD Trả lời câu hỏi Vận dụng trang 23 SGK Toán 11 Chân trời sáng tạo Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm và khoảng cách từ B đến đường kính AH là 27 cm. Tính \(\sin \alpha \) và \(\cos \alpha \), từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười.
Phương pháp giải: Quan sát hình vẽ để trả lời. Lời giải chi tiết:
Ta có: \(OA = OB = 120:2 = 60\). Xét tam giác OBB’ có: \(\sin \widehat {BOB'} = \frac{{BB'}}{{OB}} = \frac{{27}}{{60}} = \frac{9}{{20}}\). Ta có: \(\widehat {AOC} = 2\widehat {BOB'}\). Xét tam giác OCC’ vuông tại C’ có: \(\begin{array}{l}\sin \widehat {COC'} = \frac{{CC'}}{{OC}}\\ \Leftrightarrow CC' = OC.\sin \widehat {COC'} = OC.\sin \left( {2\widehat {BOB'}} \right)\end{array}\). Mà \(\sin \left( {2\widehat {BOB'}} \right) = 2.\sin \widehat {BOB'}.cos\widehat {BOB'}\). \( = 2.\frac{9}{{20}}.\frac{{\sqrt {319} }}{{20}} = \frac{{9\sqrt {319} }}{{400}}\). Vậy khoảng cách từ C đến AH là \(60.\frac{{9\sqrt {319} }}{{200}} \approx 48,2cm\).
|