Giải mục 3 trang 28, 29, 30, 31, 32 SGK Toán 11 tập 1 - Chân trời sáng tạo

HĐ4

Trả lời câu hỏi Hoạt động 4 trang 28 SGK Toán 11 Chân trời sáng tạo

Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ:

Phương pháp giải:

Sử dụng máy tính cầm tay.

Lời giải chi tiết:

HĐ5

Trả lời câu hỏi Hoạt động 5 trang 28 SGK Toán 11 Chân trời sáng tạo

Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ.

Phương pháp giải:

Sử dụng máy tính cầm tay.

Lời giải chi tiết:

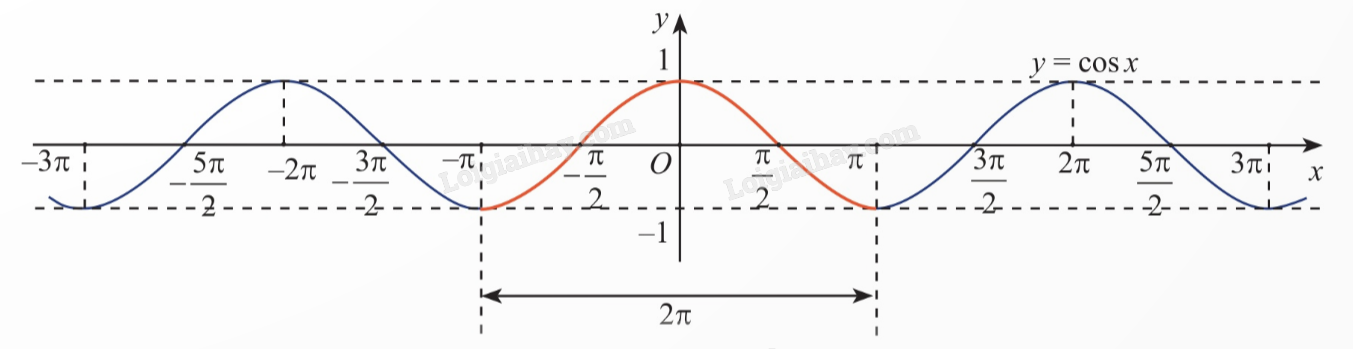
VD1

Trả lời câu hỏi Vận dụng 1 trang 30 SGK Toán 11 Chân trời sáng tạo

Li độ s (cm) của một con lắc đồng hộ theo thời gian t (giây) được cho bởi hàm số \(s = 2\cos \pi t\). Dựa vào đồ thị của hàm số côsin, hãy xác định ở các thời điểm t nào trong 3 giây đầu thì con lắc có li độ lớn nhất?

Phương pháp giải:

Dựa vào đồ thị hàm côsin để giải quyết.

Lời giải chi tiết:

Dựa vào đồ thị hàm số cosin, li độ s lớn nhất tại t = 0 và t = 2.

HĐ6

Trả lời câu hỏi Hoạt động 6 trang 30 SGK Toán 11 Chân trời sáng tạo

Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ.

Phương pháp giải:

Sử dụng máy tính cầm tay.

Lời giải chi tiết:

HĐ7

Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ.

Phương pháp giải:

Sử dụng máy tính cầm tay.

Lời giải chi tiết:

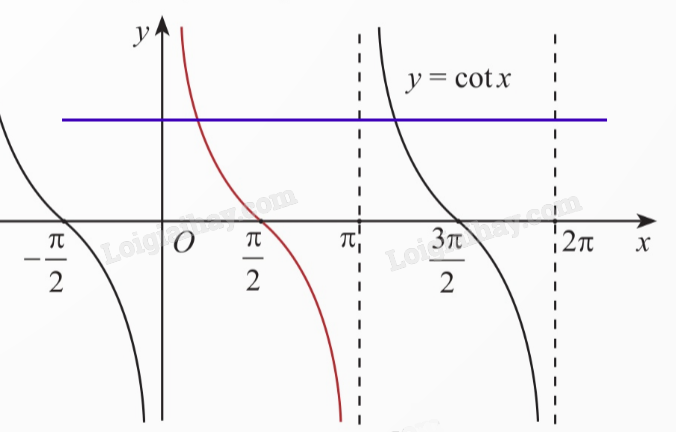
TH4

Trả lời câu hỏi Thực hành 4 trang 32 SGK Toán 11 Chân trời sáng tạo

Cho hàm số y = cotx với \(x \in \left( { - \frac{\pi }{2};2\pi } \right)\) và \(x \ne k\pi \) \(\left( {k \in \mathbb{Z}} \right)\).

a) Vẽ đồ thị hàm số đã cho.

b) Có bao nhiêu giá trị x mà tại đó giá trị hàm số đã cho bằng 2?

Phương pháp giải:

Dựa vào đồ thị.

Lời giải chi tiết:

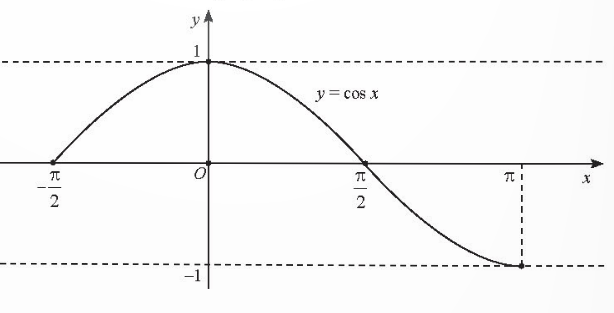
b) Có 2 giá trị x mà tại đó y = 2.

TH3

Trả lời câu hỏi Thực hành 3 trang 30 SGK Toán 11 Chân trời sáng tạo

Cho hàm số \(y = \cos x\) với \(x \in \left[ { - \frac{\pi }{2};\pi } \right]\).

a) Vẽ đồ thị hàm số đã cho.

b) Tại các điểm nào thì giá trị hàm số lớn nhất?

c) Tìm các giá trị của x thuộc \(\left[ {\frac{{ - \pi }}{4};\frac{{5\pi }}{4}} \right]\) sao cho \(\sin \left( {x - \frac{\pi }{4}} \right) < 0\).

Lời giải chi tiết:

a) Ta có đồ thị hàm số \(y = \cos x\) với \(x \in \left[ { - \frac{\pi }{2};\pi } \right]\) như hình dưới:

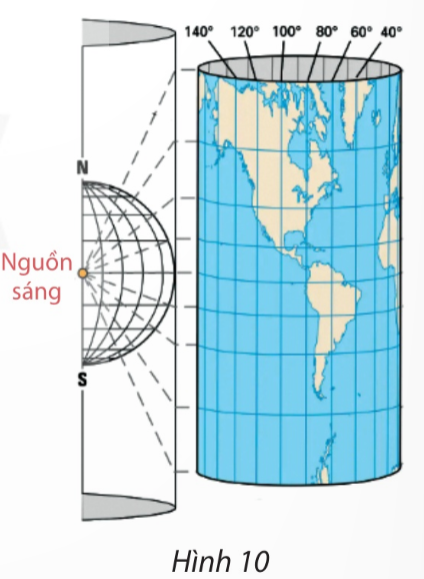
b) Tại điểm x = 0 thì giá trị hàm số lớn nhất.

c) Do \(x \in \left[ {\frac{{ - \pi }}{4};\frac{{5\pi }}{4}} \right]\) nên \(\left( {x - \frac{\pi }{4}} \right) \in \left[ {\frac{{ - \pi }}{2};\pi } \right]\).

Để \(\sin \left( {x - \frac{\pi }{4}} \right) < 0\) thì \(\left( {x - \frac{\pi }{4}} \right) \in \left[ {\frac{{ - \pi }}{2};0} \right]\).

Suy ra \(x \in \left[ {\frac{{ - \pi }}{4};\frac{\pi }{4}} \right]\).

VD2

Trả lời câu hỏi Vận dụng 2 trang 32 SGK Toán 11 Chân trời sáng tạo

Trong Địa lí, phép chiếu hình trụ được sử dụng để vẽ một bản đồ phẳng như trong Hình 10. Trên bản đồ phẳng lấy đường xích đạo làm trục hoành và kinh tuyến \({0^o}\) làm trục tung. Khi đó tung độ của một điểm có vĩ độ \({\varphi ^o}\) \(( - {90^o} < \varphi  < {90^o})\) được cho bởi hàm số \(y = 20\tan \left( {\frac{\pi }{{180}}\varphi } \right)\) (cm). Sử dụng đồ thị hàm số tang, hãy cho biết những điểm ở vĩ độ nào nằm cách xích đạo 20 cm trên bản đồ.

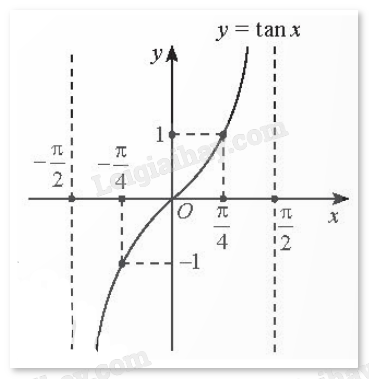
Phương pháp giải:

Vận dụng đồ thị của hàm số tan vào bài toán thực tế.

Lời giải chi tiết:

Ta có điểm nằm cách xích đạo 20cm có y = 20 hoặc y = - 20 nên \(\tan \left( {\frac{\pi }{{180}}\varphi } \right) =  - 1\).

Vì \( - {90^o} < \varphi  < {90^o}\) nên \( - \frac{\pi }{2} < \frac{\pi }{{180}}\varphi  < \frac{\pi }{2}\).

Đặt \(x = \frac{\pi }{{180}}\varphi \) với \( - \frac{\pi }{2} < x < \frac{\pi }{2}\). Ta có đồ thị:

Từ đồ thị, ta có:

y = 1 khi \(x = \frac{\pi }{4} \Leftrightarrow \frac{\pi }{{180}}\varphi  = \frac{\pi }{4} \Leftrightarrow \varphi  = {45^o}\).

y = -1 khi \(x =  - \frac{\pi }{4} \Leftrightarrow \frac{\pi }{{180}}\varphi  =  - \frac{\pi }{4} \Leftrightarrow \varphi  =  - {45^o}\).

Vậy trên bản đồ, các điểm nằm ở vĩ độ \({45^o}\) Bắc và \({45^o}\) Nam nằm cách xích đạo 20 cm.